
 |
| [ На главную ] -- [ Список участников ] -- [ Зарегистрироваться ] |
| On-line: |
| Константин Серафимов - Книжная полка / "Веревка - как она есть" Константин Б.Серафимов / 02 - Надежность |
| Страницы: 1 |


|
| Автор | Сообщение |
|
КБСыч |
Добавлено: 16-01-2005 18:33 |
|
Константин Б. СЕРАФИМОВ "ВЕРЕВКА - КАК ОНА ЕСТЬ" 2. НАДЕЖНОСТЬ ================= Оперируя только значениями прочности, мы не можем в полной мере составить представление о надежности той или иной веревки. Давайте поглубже разберемся в этом вопросе. 2.1. КОЭФФИЦИЕНТ НАДЕЖНОСТИ ВЕРЕВКИ ----------------------------------- Коэффициентом надежности веревки называется соотношение между ее минимальной практической прочностью и номинальной нагрузкой в 100 кГ - средний вес человека в снаряжении с грузом. Реальные значения коэффициента надежности для каждого конкретного куска веревки можно определить только испытаниями этого куска на разрыв. В то же время анализ зарубежных публикаций по вопросам надежности веревок, применяемых в технике SRT, показывает, что нормальными значениями коэффициента надежности можно считать величину 3,5-4,0. Речь идет о статических или близким к ним веревках, используемых при спуско-подьемных операциях, например, применяемых с целью навески или жесткой верхней страховки. Естественно, что при увеличении номинальной нагрузки (например, при работе на одной веревке двух человек) требования к практической прочности веревки пропорционально возрастают. 2.2. ДИНАМИЧЕСКИЕ НАГРУЗКИ -------------------------- Динамическими являются нагрузки, которые по величине и направлению достаточно быстро изменяются по времени. Вопреки принимаемым мерам, никогда не исключена вероятность возникновения повышенных динамических нагрузок в случаях, подобных следующим: - кратковременная потеря контроля за скоростью спуска с последующим его восстановлением (случайное проскальзывание, а затем резкое притормаживание); - проскальзывание обоих зажимов во время подъема по веревке с последующим схватыванием; - случайное западание веревки за выступ и внезапное соскакивание под нагрузкой; - неудачный старт спуска в начале отвеса или неумелое вылеэание из него с рывками веревки в непосредственной близости от основного закрепления; - разрушение опор основного или промежуточного закрепления. Последствиями этих случаев будет проскальзывание или падение находящегося на веревке человека, которого веревка должна будет удержать, - то есть возникновение динамических нагрузок, значительно превышающих допустимые при нормальной безаварийной работе. Мы не говорим о срыве при свободном лазании с динамической страховкой. Эти случаи подробно рассмотрены в альпинистской литературе. Необходимо помнить, что веревка никогда не используется независимо от остального снаряжения, которым экипированы отвесы и сам человек и образующего так называемую страховочную цепь. Страховочная цепь состоит из всех элементов снаряжения, которые в данный момент связаны посредством веревки: скала или другая базовая опора - крюк, тросовая или иная навесочная петля - карабин - веревка - ФСУ или зажим - самостраховочный "ус" или иная подвеска - карабин - беседка - тело человека. Очевидно, что нагрузки, статические или динамические, возникают во всех элементах страховочной цепи. ПОЛЕЗНО ЗНАТЬ: -------------- - Всякая цепь на столько надежна, на сколько надежно слабейшее ее звено. Страховочная цепь - тоже не исключение из этого правила. - Из всех элементов страховочной цепи наиболее подвержена износу и легко уязвима веревка. - Наибольшие динамические нагрузки возникают при разрушении основных или промежуточных закреплений, а также в случае совершения грубых технических ошибок при страховке, движении по веревке или других манипуляций с ней. Поэтому всякая работа на отвесе должна предусматривать возможность возникновения таких ситуаций, когда динамические нагрузки значительно превысят нормальные для безаварийной работы. И меры должны быть приняты заблаговременно. Тем более, что это всегда зависит от самого исполнителя. 2.3. ЭНЕРГИЯ ПАДЕНИЯ -------------------- Если подвесить тело определенного веса на конец веревки, последняя будет испытывать нагрузку по всей длине, включая и точку закрепления. Величина этой нагрузки будет равна весу подвешенного тела. Если же поднять тело на некоторую высоту и бросить, сила, которая возникнет после того, как веревка натянется, будет значительно больше. Под действием гравитации всякое падающее тело во время падения ускоряется. Это означает, что его скорость нарастает по мере увеличения расстояния от точки начала падения. В зависимости от массы и скорости в каждый момент падения тело обладает определенной энергией, которая называется ЭНЕРГИЕЙ ПАДЕНИЯ (Е). Эта энергия тем больше, чем больше масса падающего тела и его скорость. Следовательно, энергия падения зависит от веса тела (G) и от высоты (Н), с которой происходит падение: Е = GH. (Таблица 6). Таблица 6. Зависимость энергии падающего тела от высоты. -------------------------------------------------------- Высота_________Скорость_________Время____________Энергия падения Падения(м)_____падения(м\сек)___падения(сек)_____(кг\м) Н______________V________________t________________при G=80 кг при G=100 кг 1______________4.41_____________0.45_____________80____________100 2______________6.27_____________0.64_____________160___________200 3______________7.64_____________0.78_____________240___________300 4______________8.82_____________0.90_____________320___________400 5______________9.90_____________1.01_____________400___________500 Значения, приведенные в таблице, получены из формул: Vп = Vo + gt H = Vot + gt^2/2 ^ - это степень, квадрат. При условии, что начальная скорость падения принимается равной О При удержании падающего веревкой скорость падения сводится к 0. При этом энергия падения трансформируется в энергию деформации веревки и других элементов страховочной цепи, включая тело падающего. 2.4. МАКСИМАЛЬНАЯ ДИНАМИЧЕСКАЯ НАГРУЗКА ------------------------------------------- В конце свободного падения энергия тела равна произведению веса падающего тела (G) на глубину падения (Н). Чтобы остановить падение, веревке необходимо произвести определенную работу деформации (А), которая равна энергии падения (Е). Это можно проиллюстрировать на графике, показывающем зависимость удлинения веревки от величины приложенной к ней силы (Рис. 1). 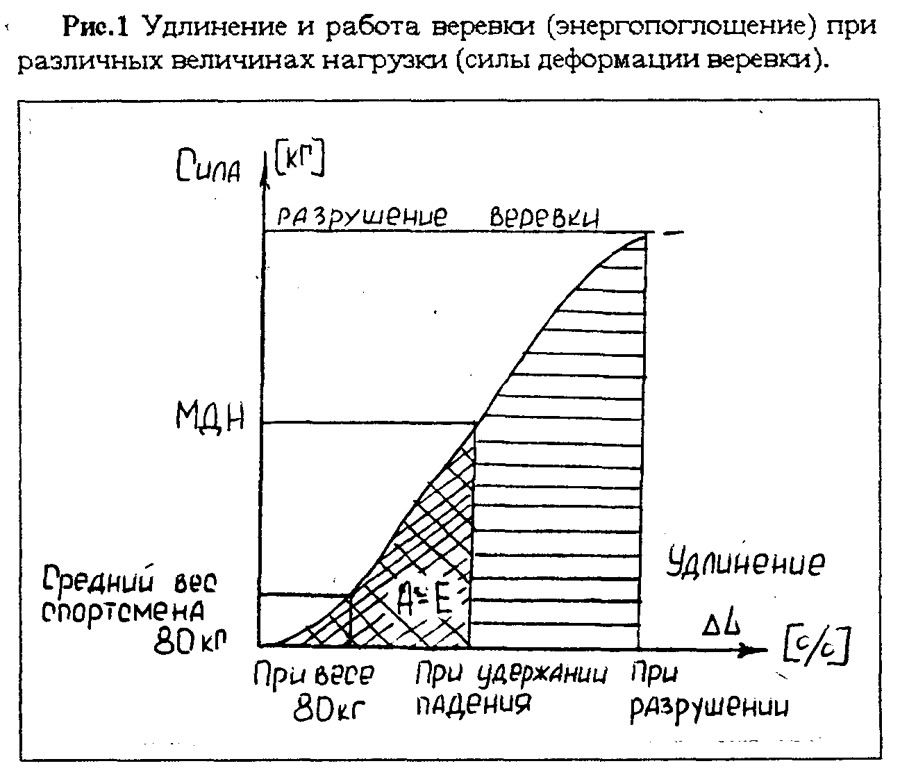 Так как работа равна величие силы помноженной на изменение пути (в нашем случае путь равен удлинению веревки), то площадь между кривой и осью абсцисс равна работе, совершенной веревкой при задержании падения. Деформация растягивающейся под действием падающего тела веревки порождает силу торможения падения, величина которой до тех пор непрерывно нарастает, пока работа торможения (А), совершаемая веревкой, не поглотит (станет равна) энергию его падения (Е). В момент остановки падения сила торможения (вызванная деформацией веревки) достигает своей максимальной величины. Максимальная величина силы торможения (которой она достигает при остановке падения) называется МАКСИМАЛЬНОЙ ДИНАМИЧЕСКОЙ НАГРУЗКОЙ (МДН). Другими словами, МДН - это максимальная величина силы динамического удара, который страховочное снаряжение и человеческое тело выдерживают в момент, когда падение уже остановлено веревкой и она перестала удлиняться. Это понятно. А вот сейчас - внимание! Величина МДН НЕ ЗАВИСИТ от абсолютной высоты падения, а определяется ТОЛЬКО фактором падения и динамическими качествами веревки. Понимание этого положения встречает определенные трудности, так как наше сознание не может смириться с мыслью, что падение, к примеру, со 100 метров приводит к такому же динамическому удару, как и падение с каких-нибудь 10 метров. Не очевидно. Тем не менее, это так, если в обоих случаях падение остановлено веревкой с одинаковыми динамическими качествами и само падение носит одинаковый характер (имеет одинаковый фактор падения). Рассмотрим эти понятия повнимательнее. 2.5. ДИНАМИЧЕСКИЕ КАЧЕСТВА ВЕРЕВКИ ------------------------------------- Под динамическими качествами веревки следует понимать, прежде всего, ее способность к удлинению. При одинаковой энергии падения МДН всегда будет ниже для веревки более эластичной и выше для веревки с меньшей способностью к удлинению (Рис.2). Экспериментально установлено, что величина максимальной динамической нагрузки зависит не от энергии падения как таковой, а, главным образом, от способности веревки удлиняться в большей или меньшей степени при данном факторе падения. 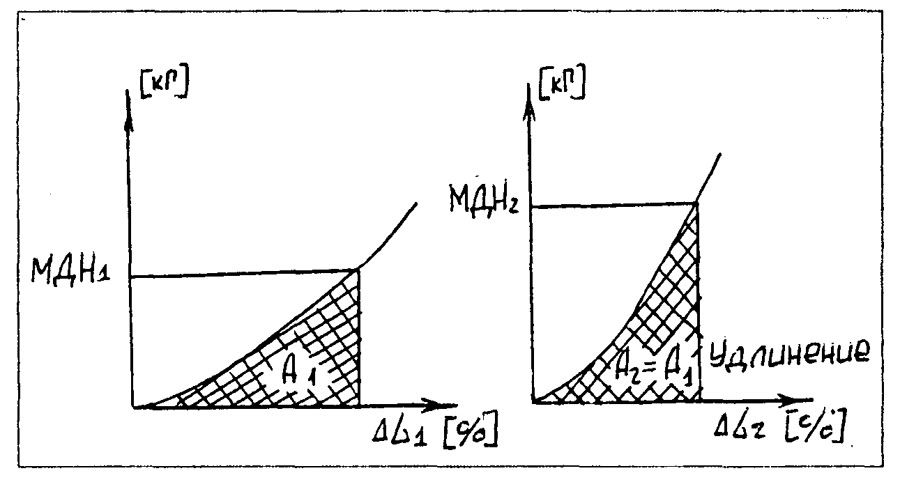 Рис.2 Зависимость МДН от динамических качеств веревки. Таким образом, представление о том, что определенной высоте падения соответствует строго определенная величина МДН столь же неверно, как и попытка рассуждать о безопасности хождения по одинарной веревке, руководствуясь только данными о ее прочности. Разные веревки имеют различные динамические качества, то есть способность удлиняться под нагрузкой. Поэтому при одинаковой высоте и факторе падения в разных веревках возникают разные величины максимальных динамических нагрузок. Более прочная, но менее эластичная веревка при удержании падения испытывает более высокую динамическую нагрузку и наоборот. Именно это положение определяет возникновение недопустимо больших динамических нагрузок при использовании стального троса в качестве линейной опоры для страховочных операций. Стальной трос имеет ничтожную способность к удлинению при нагрузке, а значит, даже малейшее падение на тросе приведет к возникновению сильного динамического удара на все элементы страховочной цепи. ПОЛЕЗНО ЗНАТЬ: -------------- - Конкретная величина МДН изменяется в широких пределах. Она не зависит от абсолютной высоты падения, как от отдельно взятой величины, а определяется исключительно динамическими качествами веревки и фактором падения. - Под динамическими качествами веревки следует понимать, прежде всего, ее способность к удлинению. 2.6. ФАКТОР ПАДЕНИЯ --------------------- Вопрос о факторе падения довольно подробно рассмотрен в альпинистской литературе, но кажется полезным напомнить читателю основные положения. В советской практике фактор падения иногда называется "коэффициентом падения". Что же такое фактор или коэффициент падения? Фактором падения называется отношение между высотой (глубиной) падения (Н) и длиной веревки (L), которая это падение останавливает: f = H/L. От этого отношения зависит так называемая "степень" или "тяжесть" падения, и, прежде всего, нагрузка на страховочную цепь при удержании веревкой падающего тела. Разберемся, почему это так. Предположим, что мы подняли тело весом P на 2 метра над точкой закрепления веревки А (Рис. 3 а). Если тело отпустить, то до того момента как веревка начнет растягиваться, глубина его падения (Н), будет равна 4 метрам, то есть двум длинам L веревки. В этом случае фактор падения равен: f = H/L = 4/2 = 2. Эта цифра означает, что при удержании падающего тела на каждый метр веревки приходится энергия, равная энергии свободного падения данного тела с высоты 2 м. То есть (предположив вес падающего равным 80 кГ): 80 кГ веса падающего, помноженные на 4 м глубины падения дадут: 80 кГ х 4 м = 320 кГм энергии падения. 320 кГм энергии падения, распределенной на 2 м длины имеющейся в распоряжении веревки: 320 кГм : 2 м = 160 кГм/м. Это означает, что каждый метр веревки за счет своей деформации должен поглотить (амортизировать) 160 кГм энергии падения. 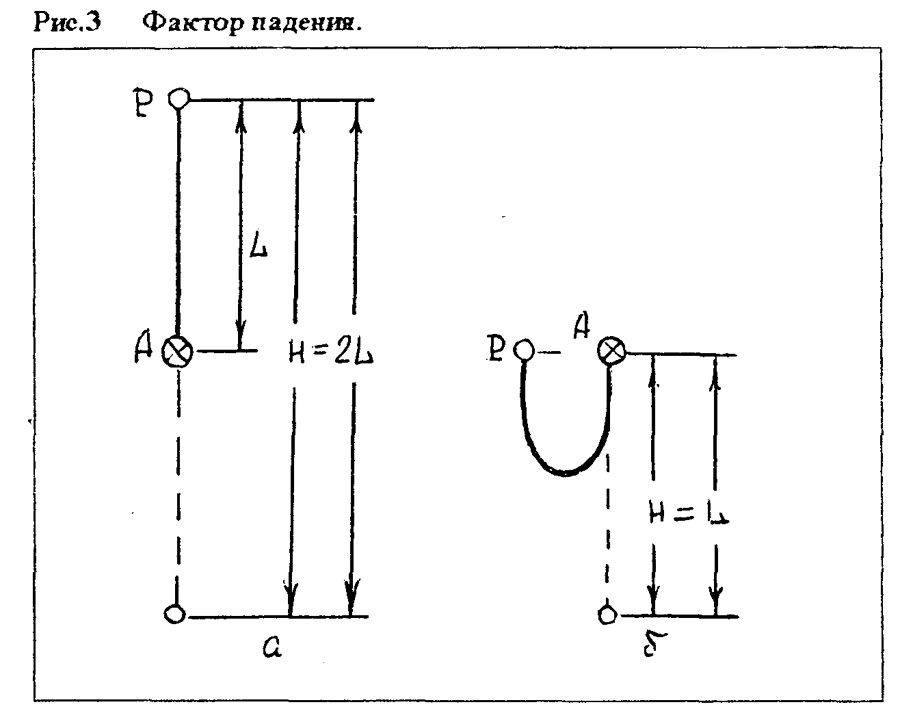 Иными словами фактор падения определяет так называемую ОТНОСИТЕЛЬНУЮ глубину падения, то есть, сколько метров свободного падения приходится на каждый метр веревки, участвующей в удержании данного падения. Энергия падения распределяется в одинаковой степени на каждый метр веревки, и каждый ее метр испытывают одинаковое элементарное относительное удлинение. Общее удлинение веревки пропорционально общей ее длине. Следовательно, способность каждой конкретной веревки поглощать энергию будет тем больше, чем больше будет ее длина. Поэтому усилия в веревке при удержании динамического рывка зависят не от абсолютной глубины падения, а лишь от ее относительной величины, - то есть от фактора падения. Подтвердим этот вывод, подняв тело Р не на 2, а на 20 м над точкой закрепления. В этом случае понадобится веревка длиной 20 м, а глубина свободного падения возрастает до 40 м. Фактор же падения в этом случае не изменится: f = 40/20 = 2 Не изменится и энергия, приходящаяся на каждый метр веревки: 80 кГ х 40 м глубины падения = 3200 кГм энергии! Однако 3200 кГм : 20 м длины веревки = 160 кГм/м. Все те же 160 кГм, которые предстоит самортизировать каждому метру веревки! Это значит, что величина нагрузки - рывка, приходящегося на веревку, останется совершенно такой же, как и при падении на глубину 4 м. Казалось бы, невероятно, но факт. Фактор падения остался одним и тем же, и нагрузки при удержании рывка не изменились, хоть полет был в десятки раз больше. Несмотря на то, что во втором случае энергия падения в 10 раз больше, но она и распределяется по веревке в 10 раз большей длины, а значит имеющей в 10 раз бОльшую способность поглощать энергию. Значит, при одном и том же факторе падения работа торможения, производимая в процессе деформации каждым метром веревки, независимо от абсолютной глубины падения, будет одинакова. Поэтому и величина МДН (максимальной динамической нагрузки) для данной веревки будет одинаковой как при падении на 2 метра, так и на 10 метров. Каким бы странным и не очевидным это ни казалось. То есть при равных остальных условиях (масса тела, динамические качества веревки и пр.), величина максимальной динамической нагрузки, возникающей в момент остановки и зависания на веревке падающего тела не зависит от абсолютной глубины падения, а зависит только от его фактора. Чем меньше окажется фактор падения, тем меньше будет величина динамического рывка и наоборот. Во втором примере (Рис. 3 б) глубина свободного падения равна длине веревки, то есть срыв произошел от точки закрепления веревки. При таком раскладе фактор падения будет: f = 2/2 = 1. В этом случае нагрузка на страховочную цепь и главную ее составляющую - веревку, будет значительно меньше, так как каждый ее метр будет амортизировать энергию падения того же тела, но с высоты всего 1 метр: 80 кГ веса х 2 м глубины падения = 160 кГм энергии; 160 кГм : 2 метра веревки = 80 кГм/м на каждый метр веревки. Вдвое более легкие условия. Максимальный фактор падения - 2. Это наиболее тяжелая степень падения на глубину, равную двойной длине веревки. Вероятность такого падения никогда не исключена при свободном лазании, если первый в связке срывается в момент, когда веревка между партнерами еще не закреплена на промежуточных крючьях. Однако если не говорить о восхождениях с нижней страховкой, при правильно оборудованных отвесах возможные падения всегда будут много более низкой степени: в большинстве случаев фактор падения не превышает значений 0,3-0,5. Именно это позволяет в практике вертикальной спелеологии и при спасательных операциях применять мало эластичные, так называемые, статические веревки и стальной трос. В принципе, при восхождениях с нижней страховкой возможны падения лидера связки с фактором даже превышающим максимальное значение 2. Если после срыва лидера, страхующий умудрится несколько выбрать страховочную веревку, а потом жестко закрепить ее без протравливания, то на каждый ее метр придется энергия выше, чем обычные 2 к 1. Но в реальных условиях это очень маловероятно. Каким образом мы можем влиять на величину фактора падения? Прежде всего, грамотно навешивая веревку. Следует внимательно следить за тем, чтобы длина используемой веревки всегда была сопоставимой с глубиной возможного падения в случае каких-либо неприятностей на отвесе. Во-вторых, не попадая в положения, когда возможны тяжелые падения. То есть не выходя над точкой закрепления веревки без серьезной к тому необходимости. Именно величина фактора возможного падения всецело находится в наших руках. Поэтому и о значениях максимальной динамической нагрузки, возникающей в страховочной цепи, следует говорить только для данной, заданной нашими сознательными действиями, величины фактора падения. К примеру, значения МДН для динамической альпинистской веревки приводятся в ее паспортах для фактора падения 1,78, что соответствует среднестатистической ситуации срыва и падения лидера связки при восхождении с нижней динамический страховкой. Значения же МДН для статических спелеоверевок определяются для фактора падения 1,0, то есть наиболее вероятного максимального фактора падения при разрушении точек закрепления навески и т.п. Следует иметь ввиду, что приводимые в паспортах веревок значения МДН определяются для ПЕРВОГО испытательного рывка. Важно понимать, что если веревку, выдержавшую динамический удар, использовать для удержания еще одного падения, аналогичного первому, то при этом величина максимальной динамической нагрузки неизбежно возрастет, так как при первом рывке часть волокон будет необратимо деформировано, и ее динамические качества веревки несколько ухудшатся. Именно поэтому опытные восходители по возвращении с горы немедленно заменяют веревку, если ею был остановлен хотя бы один серьезный срыв. И правильно делают. 2.7. ГРАНИЦА Но ("Аш-нулевое") --------------------------------- Как видно из Рис.4 сила нагрузки на веревку до тех пор не может достичь максимума для данного фактора падения, покуда длина веревки (L), а соответственно и высота падения (Н), будут меньше некоторой минимальной величины. Это так называемая граница Но, после которой величина МДН входит в соответствие с величиной фактора падения. Почему это происходит? 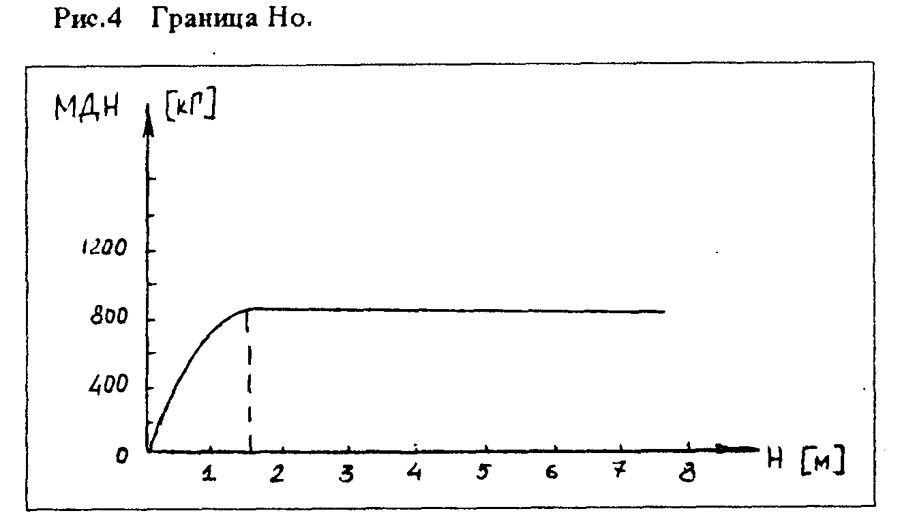 Осуществим ряд последовательных падений одного и того же груза с фактором 1, но в каждом последующем случае будем останавливать его падение все более длинным куском веревки. Если измерить величины возникающих при этом динамических нагрузок, то мы получим кривую, которая вначале стремительно идет вверх, а затем все более выполаживается, пока не достигает некоей границы Но (Рис.5). После этого график превращается в линию параллельную оси абсцисс: МДН стала постоянной, то есть такой, какой она и должна быть в случае, когда фактор падения тоже постоянен. 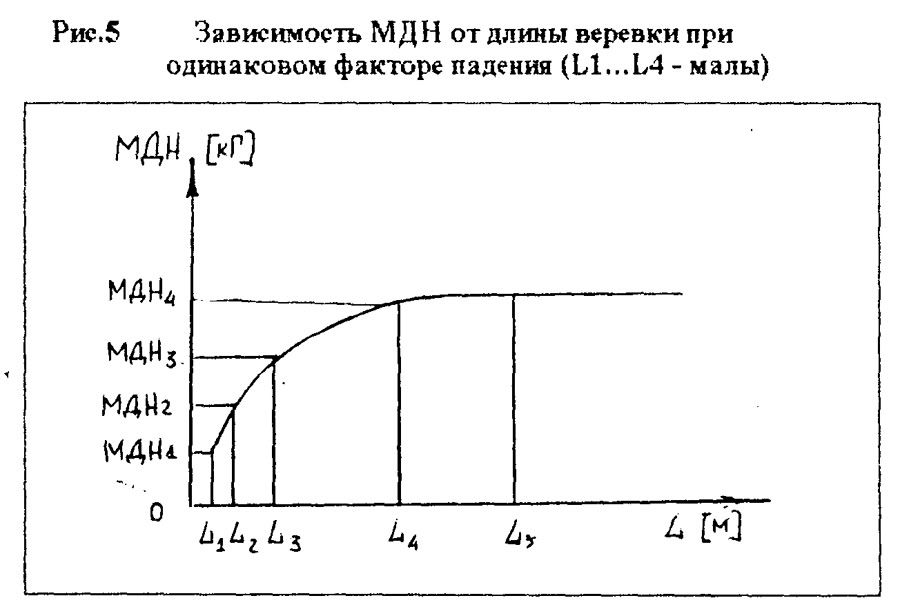 Полезный эффект снижения величины МДН, действующей на веревку при ее длине, меньшей границы Но, отчасти объясняется тем, что часть энергии падения поглощается трением между витками узлов и деформацией составляющей узлы веревки. При небольших глубинах падения эта часть сопоставима с общей энергией падения. Таким образом, доля узлов в общем энергопоглощении достаточно значительна и поэтому заметна. При больших глубинах падения узлы точно также амортизируют часть энергии падения, но доля их на, общем фоне становится пренебрежимо мала. Однако отметим этот факт: узлы на веревке амортизируют часть энергии падения. Эффект границы Но имеет практическое значение для коротких кусков веревки, снижая возможные динамические нагрузки. Например, в случае с самостраховочными "усами", или для участков веревки, связывающих основные и дублирующие закрепления. Поэтому не стоит стремиться затягивать узлы усилием, превышающим вес человека. Величина границы Но непосредственно зависит от вида веревки, а также от ее состояния - мокрая или сухая, более или менее изношенная и т.п. В целях практической работы можно принять, что для динамических веревок их длина, при которой сколько-нибудь заметно проявляется эффект границы Но, будет порядка 1,5 м, а для статических веревок - не более 1 м с учетом завязанных на конце веревки узлов. 2.8. ВРЕМЯ ОСТАНОВКИ ПАДЕНИЯ. ИМПУЛЬС СИЛЫ ----------------------------------------------- Для абсолютно твердого тела, падающего на абсолютно твердую поверхность, то есть при абсолютном отсутствии эластичных элементов, время удара о поверхность стремится к 0, а его сила - к бесконечности. В реальных условиях все несколько мягче. Благодаря наличию эластичных элементов в страховочной цепи, и, прежде всего, веревки, остановка падения не происходит мгновенно: для погашения энергии падения необходимо некоторое время. Сила удара (максимальная динамическая нагрузка), также не является беспредельной, а зависит, как мы уже говорили, от динамических качеств веревки и фактора падения. Произведение величины силы на время ее действия называется ИМПУЛЬСОМ СИЛЫ. Если максимальная динамическая нагрузка (при заданном факторе падения) является постоянной и не зависит от абсолютной высоты падения (Н), импульс силы, напротив, зависит от высоты падения и нарастает с увеличением скорости падающего тела. Более длинная веревка остановит наше падение за большее время, по сравнению с короткой. Например, если для падения с высоты H1 необходимое время остановки падения будет равно T1, а для Н2 - Т2, и отношение высот равно Н2/H1 = R, то отношение времен торможения до полной остановки будет T2/T1 = квадратный корень из R. То есть если при падении с высоты Н1 = 1 м для остановки падения понадобится время T1 = 0,2 сек, то время остановки падения Т2 на глубину Н2 = 9 м будет равно: H2/H1 = R = 9/1 = 9 T2/T1 = корень квадратный из 9 = 3 Т2 = 3T1 = 3 Х 0,2 сек = 0,6 сек То есть для остановки падения нужно в три раза более продолжительное время. Следовательно, более высоким и продолжительным будет и импульс силы (Рис. 6). 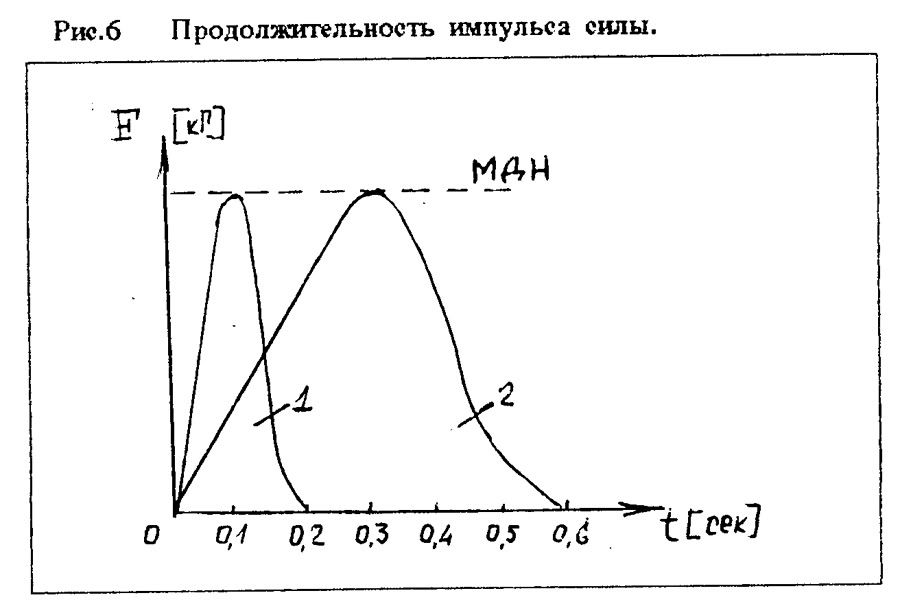 Иллюстративно кривые на рисунке - это изменение величины тормозящей силы и в то же время ускорения-перегрузки, останавливающих падающего, а импульс силы в обоих случаях соответствует площади, ограниченной кривой нарастания и падения нагрузки-ускорения. Время действия тормозящих ускорений и импульса силы не имеет значения для веревки, Но для человека вовсе нежелательно, чтобы нагрузка на него действовала более продолжительное время. При малой величине произведения приложенной силы на время удара, то есть при кратком импульсе силы, человеческое тело легко выдерживает большие нагрузки. Эта же нагрузка, но при более продолжительном импульсе силы, то есть при большем значении произведения величины приложенной силы на время ее действия, может привести к много более тяжелым последствиям. Вопрос влияния импульса силы, ускорений и перегрузок на организм человека достаточно хорошо изучен специалистами в области летательных аппаратов и сопутствующих сфер медицины. В рамках этой работы не представляется возможным детально разбираться в тонкостях этих понятий. Очевидно лишь то, что конструкция современных веревок ограничивает величину усилий, воздействующих на человека величиной максимальной динамической нагрузки, а время этого воздействия весьма мало, так как МДН возникает лишь в самом пике - в мертвой точке остановки падения, после чего быстро ослабевает. Иными словами импульс силы, возникающей при срыве на веревке вполне переносим и достаточно безопасен. ПОЛЕЗНО ЗНАТЬ: -------------- - При падении с большой высоты возникающая сила торможения действует на тело, удерживаемое веревкой, более продолжительное время. 2.9. ФАКТОРЫ, СНИЖАЮЩИЕ НАГРУЗКУ ПРИ ПОГАШЕНИИ ДИНАМИЧЕСКОГО УДАРА ==================================== До настоящего момента, мы рассматривали нагрузки на веревку при поглощении динамического удара в процессе остановки свободно падающего тела. На практике условия для такого падения возникают крайне редко. Обычно падение сопровождается ударами той или иной силы или трением тела человека о рельеф. Это до известной степени снижает скорость, а, следовательно, и энергию падения. Во-вторых, веревка не является единственным элементом страховочной цепи, который в состоянии поглощать энергию. Если участие карабинов, крючьев и другого металлического снаряжения в этом процессе незначительно, то это не относится к узлам, которые затягиваются, к самостраховочному "усу", который удлиняется, к подвесной системе, лента которой тоже не статична, и, наконец, к мускульной массе человека, которая тоже имеет известную эластичность. Все эти факторы вместе взятые, хоть и незначительно, но увеличивают общую степень деформации страховочной цепи и тем самым способствуют уменьшению величины максимальной динамической нагрузки. Например, экспериментально установлено, что если падение твердого тела весом 80 кГ с некоторой высоты на данной веревке вызывает максимальную динамическую нагрузку 720 кГ, то падение человека той же массы при тех же условиях вызовет максимальную нагрузку не превышающую 550 кГ. Это значит, что в данном случае мускульная масса человека и его подвесная система смогли поглотить около 25% энергии динамического удара. Эффект снижающих МДН факторов проявляется сколько-нибудь ощутимо лишь при падениях на малую глубину. В частности, с этим связано бытующее среди большинства альпинистов, спелеологов и спасателей представление о безопасности малых падении на небольшую глубину с зависанием на самостраховке. Порочность такого представления заключается в том, что безопасность связывается именно с малой глубиной падения, а не с пониманием смягчающих исход падения факторов, таких как амортизирующие свойства тела человека и страховочного снаряжения. Однако амортизирующие свойства страховочного снаряжения могут значительно меняться в зависимости от конструкции, материалов и состояния. То есть, в зависимости от конкретной ситуации, при той же малой глубине падения могут возникнуть различные динамические нагрузки, которые могут привести и к самым различным, зачастую печальным, последствиям. При большой глубине падения следует рассчитывать только на эффект удлинения веревки. ПОЛЕЗНО ЗНАТЬ: -------------- - При поглощении динамического удара из всех элементов страховочной цепи наиболее сильно деформируется веревка. Следовательно, она поглощает наибольшую часть энергии падения. - Узлы, самостраховочный "ус", мускульная масса и прочее уменьшают силу динамического удара, но заметно это лишь при падениях на малую глубину. - Следует заботиться не только о прочности своего снаряжения, но и о его энергопоглощающих свойствах. 2.10. НАДЕЖНОСТЬ СТАТИЧЕСКИХ ВЕРЕВОК ------------------------------------- Если мы считаем, что теперь достаточно представляем себе практическую прочность веревки, равную некоторой величине силы, под действием которой веревка с завязанными узлами, мокрая, заглиненная и т.п. рвется, то это не совсем так. Этого представления недостаточно для определения надежности, если говорить о силе, приложенной статично. С точки зрения безопасности никакого значения не имеет, какую статическую нагрузку выдерживает веревка, если при падении человека возникает динамическая нагрузка, превышающая способность какого-либо из звеньев страховочной цепи или самого человека противостоять ей. С другой стороны, любая, даже самая прочная, веревка не выдержит, если низкие динамические качества ее приведут к возрастанию динамической нагрузки до величины, превышающей практическую прочность веревки. Таким образом, надежность веревки не зависит от ее практической прочности как от отдельно взятой величины, а определяется: 1. Разностью между величиной силы, необходимой для того, чтобы довести веревку (с узлами, грязью, влагой и другими неблагоприятными факторами) до разрушения, и величиной максимальной силы динамического удара, возникающей при удержании падения. Другими словами - надежность веревки определяется разностью между ее практической прочностью и величиной возможной максимальной динамической нагрузки (Рис. 7). 2. Условием, что МДН при срыве никогда не превысит прочности остальных звеньев страховочной цепи, включая и тело человека. 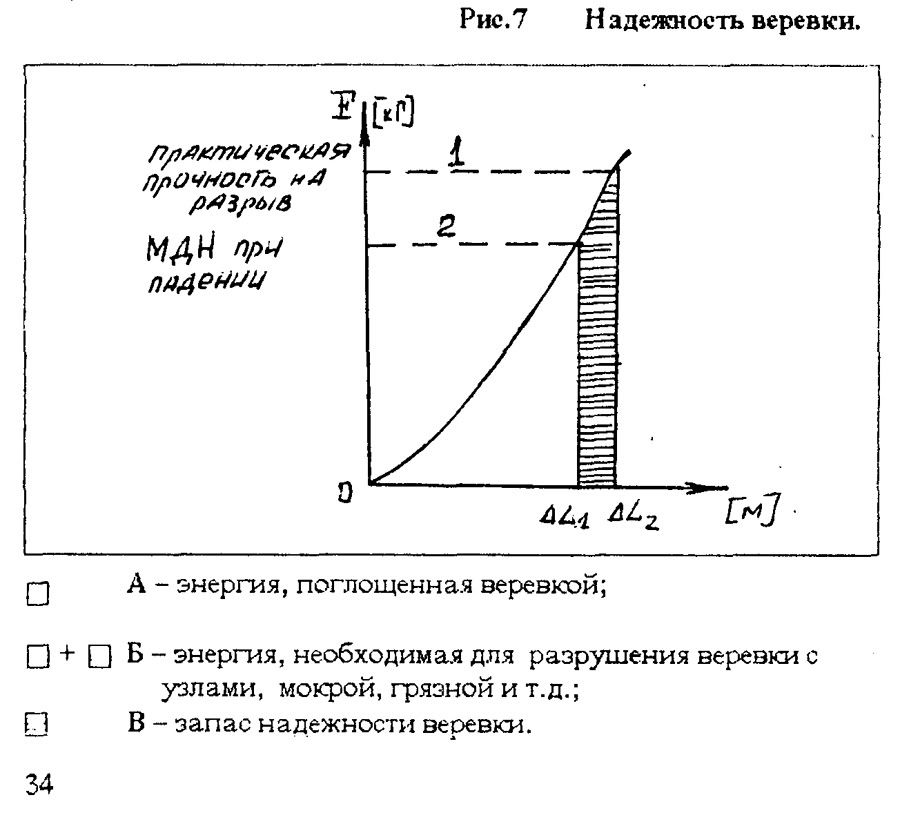 Чем более величина МДН (2) приближается к величине практической прочности веревки (1), тем меньше становится зона "В", то есть тем меньше надежность веревки и наоборот. Можем ли мы влиять на надежность нашей веревки? И если можем, то как? Ответ однозначен - можем. Прежде всего, грамотно выбирая веревку. Каждая веревка должна использоваться только в тех целях, для которых она предназначена. Глупо и опасно использовать статическую веревку для нижней динамической страховки или динамик для натягивания переправ и троллеев. Важнейшей характеристикой веревки, наряду с прочностью, является ее эластичность. Способность каждой веревки удлинятся - величина объективная. Ее можно определить, но изменить невозможно. Заложенная производителем, она будет больше или меньше, в зависимости от типа веревки и степени ее износа (см. Таблицу 5). Во-вторых, мы можем влиять на величину фактора падения, а через нее и на величину максимальной динамической нагрузки. При навеске снаряжения на отвесы необходимо безошибочно вводить величину фактора возможного падения в границы, соответствующие динамическим качествам применяемой веревки. Тогда в случае инцидента величина МДН останется ниже границы практической прочности веревки, и страховочная цепь уцелеет. А для того, чтобы иметь возможность сознательно и квалифицированно работать на вертикалях, необходимо четко понимать все процессы и закономерности, происходящие в снаряжении при работе с ним. Только таким образом мы можем гарантировать надежность веревки. ПОЛЕЗНО ЗНАТЬ: -------------- - Чистая иллюзия рассчитывать надежность одинарной веревки, исходя только из того, что данные о величине ее практической прочности в 2, 3 или более раз превышают максимально ожидаемые усилия, не имея никакого представления о ее динамических качествах. |
| Страницы: 1 |


|
| Константин Серафимов - Книжная полка / "Веревка - как она есть" Константин Б.Серафимов / 02 - Надежность |