
 |
| [ На главную ] -- [ Список участников ] -- [ Правила форума ] -- [ Зарегистрироваться ] |
| On-line: |
| средневековые замки / разное / Оптические иллюзии, виртуальные миры и др. математика |


|
| Автор | Сообщение |
|
Renata великий магистр Группа: Главный администратор Сообщений: 2765 
|
Добавлено: 21-09-2004 19:59 |
|
Фракталы http://mathworld.wolfram.com/Fractal.html http://www.nsu.ru/mmf/tvims/chernova/fract/fr.html и как их делают http://www.arbuz.uz/x_complex.html http://home.ural.ru/~shabun/fractals/fractals.htm 3D Fractals http://fractals.nsu.ru/ Ссылки http://fractals.chat.ru/   
|
|
|
Renata великий магистр Группа: Главный администратор Сообщений: 2765 
|
Добавлено: 02-10-2004 16:55 |
Зрительные иллюзии и феномены  (кого вы видите – Св. Георгия или античного юношу?) http://www.optifarm.ru/content/?sid=66 http://www.psy.msu.ru/illusion/ http://imp-world-r.narod.ru/contents.html http://www.sandlotscience.com/Impossible/impos_frm.htm http://www.sfrusforum.com/phpBB2/viewtopic.php?t=291&postdays=0&postorder=asc&start=0 http://www.kfki.hu/~nyikos/3d/00.html (на венгерск.) http://www.ilusaodeotica.com/ (на португал.) http://figuresambigues.free.fr/ (на франц.) Занимательный мир чисел, слов, пикселей и заблуждений http://www.arbuz.uz/ И обязательно обратите внимание на работы художника Маурица Эшера в этой теме нашего форума (мои посты от 30-09-2004 02:18 и 01-10-2004 04:47 . Искусственные пейзажи http://www.planetside.co.uk/terragen/gallery/gallerymain.php http://www.renderosity.com/gallery.ez?ByArtist=Yes&Artist=morbidorbits |
|
|
Роман великий магистр Группа: Модераторы Сообщений: 1557 
|
Добавлено: 13-10-2004 19:04 |
| Математика в лицах http://www.univer.omsk.ru/omsk/Edu/Math/index.htm | |
|
Galina великий магистр Группа: Участники Сообщений: 905 
|
Добавлено: 16-02-2005 20:35 |
|
Картинки-иллюзии. Прекрасное собрание. Темы: Невозможное Восприятие цвета Зрительные искажения Распознавание образов Двойственные образы Иллюзии движения Восприятие размера Перевертыши Восприятие глубины Приколы  http://www.log-in.ru/ и входная страничка очень симпатичная |
|
|
Renata великий магистр Группа: Главный администратор Сообщений: 2765 
|
Добавлено: 27-02-2005 21:31 |
| Как читать римские числа http://www.doktor.ru/latin/numer/lat_num.htm | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 07-06-2005 02:18 |
|
Оптические иллюзии http://www.ritsumei.ac.jp/~akitaoka/index-e.html http://www.panoptikum.net/optischetaeuschungen/opticalillusions.htm |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 06-07-2005 04:26 |
|
Оптическая иллюзия http://mikel.altonika.ru/Illusion/index.html http://www.michaelbach.de/ot/col_rapidAfterimage/index.html Юмор на тему этой иллюзии http://www.livejournal.com/users/uster/165579.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 07-07-2005 02:53 |
| Скрещивание флоры и фауны в Фотошопе http://www.worth1000.com/cache/contest/contestcache.asp?contest_id=6264&display=photoshop#entries | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 08-10-2005 20:55 |
 1 - Cмотря на одну точку Вы заметите, что квадраты начинают покачиваться, а потом двигаться. 2 - Если выбрать одну ячейку, то мозг очертит квадрат 5x5 (или какого-либо другого размера) вокруг этой ячейки. Если взгляд переместить на любой другой квадрат, то Вы увидите очертание совсем другого квадрата.) Еще иллюзия: http://intrance.ru/media/i/expansion.gif Мастер иллюзий Akiyoshi Kitaoka http://www.ritsumei.ac.jp/~akitaoka/index-e.html |
|
|
Роман великий магистр Группа: Модераторы Сообщений: 1557 
|
Добавлено: 30-10-2005 02:38 |
| Иллюзия http://www.livejournal.com/users/sklyarevskiy/79064.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 01-11-2005 03:38 |
|
Смотрите на это изображение (слева монстрик, справа женщина) и отходите от монитора (в зависимости от остроты зрения - 1-3 метра),слева будет женщина, а монстрик справа. http://www.livejournal.com/users/kkirsanov/156451.html Еще иллюзии:  
|
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 27-12-2005 23:24 |
|
Dragon Optical Illusion http://www.grand-illusions.com/dragon.htm Вот здесь можете скачать себе выкройку этого зверя: http://www.kevinhowlett.com/other/dragon.jpg |
|
|
Роман великий магистр Группа: Модераторы Сообщений: 1557 
|
Добавлено: 17-01-2006 02:19 |
| Генератор случайных чисел http://www.homesoft.ru/rus/lotto/generator.shtml | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 25-01-2006 20:59 |
|
Коллекция оптических иллюзий - более 2400 штук: невозможные фигуры, цветовые иллюзии, зрительные искажения, двойственные образы, иллюзии движения, перевертыши, стереоиллюзии, приколы и так далее. Но и кроме иллюзий там хватает, что посмотреть и чем развлечься: занимательные головоломки, психологические тесты, интересные факты, статьи о необычных явлениях и развивающие онлайн-игры. http://www.log-in.ru/ |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 25-04-2006 04:25 |
|
Музей невозможных вещей: http://www.lhup.edu/~dsimanek/museum/unwork.htm А вот еще одна библиотека невозможного, на русском: http://imp-world-r.narod.ru/russian/index.html |
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 09-05-2006 17:24 |
Как можно так нарисовать, чтобы при отражении от цилиндра появилось изображение http://mightyillusions.blogspot.com/2006/05/cylinder-mirror-optical-illusion.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 31-05-2006 03:07 |
|
Порой не всё такое, каким оно кажется нам. А может быть нам просто хочется, чтобы оно было другим? Если вы ещё не видели его, обязательно посмотрите прекрасный сайт, посвящённый оптическим и зрительным иллюзиям Например, это — лишь роза? http://www.psy.msu.ru/illusion/ http://toster.livejournal.com/56332.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 10-06-2006 02:12 |
|
Если секунд 10-20 смотреть в точку в центре этого изображении храма Василия Блаженного, а затем, не отводя глаз, навести на картинку курсор мышки, то перед вами появится нормальная цветная фотография, которая моментально станет черно-белой, стоит вам слегка посмотреть в сторону. http://masterblog.front.lv/hvb/ |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 13-06-2006 03:29 |
|
В то время, когда вы тут по Интернету шастаете, вместо того чтобы работать, австралийский художник (а заодно и композитор) Питер Миллер (Peter Miller) натворил вот такие картинки. Не знаю, что вам кажется, но тут нет никакой эротики — сплошная математика: все изображения являют собой графическое отражение математических формул. http://willbe.livejournal.com/165203.html Анимированные математические функции http://sprott.physics.wisc.edu/fractals/animated/ |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 19-06-2006 00:45 |
| Программа для создания калейдоскопов Скачать тут 150 кб http://barbaris.uz/temp/kaleidoscope_4.rar | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 21-06-2006 05:13 |
|
Среди огромного количества открытий и изобретений (обычную привычную тачку придумал Паскаль) одним из самых приятных и волнующих всех любителей математики остается треугольник, названный именем автора. Элементарнейший закон, по которому каждое число равно сумме двух, стоящих над ним приводит к бесконечной россыпи таинственных и неожиданных закономерностей. В треугольнике найдете биноминальные коэффициенты, треугольные и тетраэдальные числа, числа Фибоначчи, он поможет уложить пятимерные шары в пятимерном же пространстве и моментально решить задачи по комбинаторике. Однако главная для любителей математических картинок изюминка треугольника Паскаля проявляется при попытке раскрасить его числа в зависимости от их делимости. Если, например, выводить четные числа черным цветом, а нечетные белым — сразу ахнем от удивления, увидев знаменитый треугольник Серпинского. Если же брать зависимости посложнее, например, делящиеся на 7 выводить красным цветом, кратные пяти зеленым, а кратные трем — синим, то каждый раз будем получать потрясающие по красоте правильные узоры. Если есть желание попрограммировать и поиграть с треугольником Паскаля и узнать о нем побольше http://sklyarevskiy.livejournal.com/290593.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 25-06-2006 03:41 |
| Картины – оптические иллюзии http://ziza.ru/2006/06/23/opticheskie-illyuzii.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 07-08-2006 04:03 |
| «Календромы» http://sklyarevskiy.livejournal.com/213338.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 18-08-2006 03:55 |
|
Кому тесно в двоичной системе http://www.infoverse.org/octomatics/octomatics.htm http://mi3ch.livejournal.com/878697.html  
|
|
|
Valerij великий магистр Группа: Администраторы Сообщений: 3753 
|
Добавлено: 16-09-2006 20:57 |
| Оптический обман http://doci.nnm.ru/ex_garmoshechka/12.09.2006/opticheskij_obman_1/ | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 19-09-2006 04:25 |
|
Очередной сайт, посвященный оптическим иллюзиям. Здесь уже иллюзии аккуратно разделены на категории. От традиционных до сложных рисованных вроде этой: http://www.grand-illusions.com/opticalillusions/ |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 21-10-2006 06:00 |
|
Оптический обман. Держите крышу. Квадраты A и B имеют одинаковый тон серого. Для проверки можно распечатать картинку и вырезать их ножницами. Или поверить на слово. 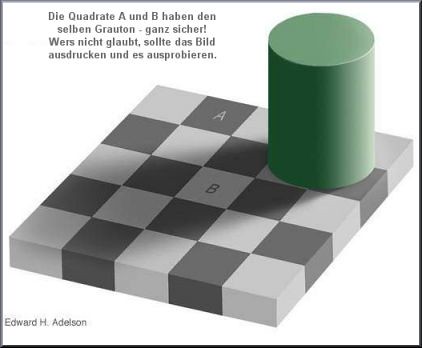 Все просто. Тени затемнены практически до черного и если их убрать, все сразу понятно. 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 08-11-2006 07:25 |
|
Аннотация к книге: Говорят, для того чтобы поверить, надо увидеть, а что, если в увиденное невозможно поверить? "Оптические иллюзии" - это занимательная коллекция визуальных трюков, парадоксов, головоломок и загадочных картин, которая удивит и увлечет вас если не объяснением того, почему это все "работает", то, по крайней мере, своим содержанием. Ставящие в тупик сочетания форм, призывающие вас искать в них спрятанные фигуры, поразительные графические изображения, которые заставляют вас недоверчиво трясти головой, искуснейшие картины, на которых вы, не веря своим глазам, пытаетесь еще и еще раз сосчитать обманчивое количество лиц, рук и ног, - все то, что делает обычное изображение необычным. Этот сборник 75 цветных и черно-белых оптических иллюзий из известной коллекции "Illusion Works" позволит вам увидеть результаты труда объединенных под этой маркой специалистов, а также насладиться некоторыми классическими иллюзиями. Приготовьтесь к тому, что книга не только позабавит, но и озадачит вас! http://community.livejournal.com/kniga_file/84784.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 09-11-2006 06:03 |
|
Даниэль Эрдели (Daniel Erdely), венгерский художник и дизайнер, придумал спидроны в 1970-х годах. Началось всё с того, что он нарисовал фигуру в виде двух “завитков”, собранных из треугольников. Отдалённо эта структура напоминает рукава или бар галактики, но стали ли источником вдохновения астрономические наблюдения — неизвестно.Каким образом Эрдели создал это изображение? У спидрона Эрдели обнаружил интересное свойство: площадь любого равностороннего треугольника в любом рукаве равна сумме площадей всех последующих меньших треугольников. Другими словами, в равносторонний треугольник можно вписать все остальные, которые строились после него.Однако вскоре он открыл более впечатляющие особенности спидронов. Если вырезать эти фигуры из бумаги и сгибать их по граням, то они могут складываться наподобие мехов аккордеона. Интересно и то, что множество таких, теперь уже трёхмерных, спидронов можно использовать для создания самых разнообразных рельефных поверхностей. Более того, оказалось, что если сделать небольшое отверстие в месте соединения спидронов, то их движение происходит намного проще. А это значит, что рельеф поверхности, собранной из них, может легко изменяться.В 1979 году Эрдели решился показать изобретение своему преподавателю Эрно Рубику (Ernö Rubik) — тому самому, что придумал небезызвестный кубик. Эрно очень удивился и сказал, что никогда не видел ничего подобного. После столь авторитетной оценки Эрдели, конечно, очень обрадовался и решил продолжить работу с геометрией спидронов. Ведь если к “спидроновому рельефу” приложить усилие, то спидроны начнут скручиваться, из-за чего механическое напряжение поверхности усилится, и поверхность будет как бы пружинить. Поэтому такие структуры можно использовать, к примеру, в качестве амортизаторов, для изготовления шумопоглощающих покрытий или, скажем, для создания тонких, но не ломающихся солнечных панелей. Вдобавок ко всему Эрдели уверен, что его изобретение можно применять и в производстве игрушек, а также в качестве строительных материалов. http://sklyarevskiy.livejournal.com/466928.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 15-11-2006 06:11 |
|
КНИГА ПО ТЕМЕ (И. Добеши) Десять лекций по вейвлетам. Книга представляет собой введение в курс вейвлет-анализа, имеющего приложение в теории временных рядов, методах распознавания образов и пр. Она является одним из лучших введений в эту область современной математики, за эту книгу Ингрид Добеши была награждена премией Лероя Стила Американского Математического Общества. http://community.livejournal.com/kniga_file/136577.html |
|
|
Valerij великий магистр Группа: Администраторы Сообщений: 3753 
|
Добавлено: 23-11-2006 16:00 |
|
3 ноября 1906 на Второй международной конференции по беспроволочной телеграфии в Берлине в качестве международного сигнала бедствия на море был принят сигнал три точки — три тире — три точки (в азбуке Морзе: ... — — — ...). Сначала сигнал не имел буквенного эквивалента. Однако поскольку в международно признанном к тому моменту варианте азбуки Морзе буква S кодировалась последовательностью трех точек, а O — трех тире, то сокращение SOS, помогавшее запомнить сигнал, напрашивалось само собой. Впрочем, впервые оно появилось в 1907 г., уже после принятия сигнала, в газетном отчете о конференции. Конвенция, подписанная в Берлине, вступила в силу 1 июля 1908 г. Первым кораблем, пославшим сигнал SOS, был трансатлантический лайнер «Slavonia», налетевший на рифы близ Азорских островов на пути из Нью-Йорка в Триест. Это произошло 10 июня 1909 г. Выживает сильнейший: SOS и его конкуренты SOS был не единственным кандидатом на роль общепризнанного сигнала бедствия. Души спасены не будут: тайна слова из трех букв Несмотря на то, что сигнал был изначально придуман в Германии как удобная, легко запоминающаяся и легко узнаваемая последовательность точек и тире, в народной памяти бытуют преимущественно английские варианты расшифровки этого «сокращения». Такие ретроспективные интерпретации, основанные на мифах о происхождении сокращений (акронимов) и сходных с ними буквенных кодов, получили названия бэкронимов (гибрид из «back» и «acronym»). Среди наиболее известных бэкронимов SOS: Save Our Souls (спасите наши души), Save Our Ship (спасите наш корабль), Survivors On Ship (выжившие на корабле) и т. п. Все они однако представляют собой не более, чем удобные фразы, придуманные для запоминания сигнала. Майский день, не предвещающий ничего хорошего С появлением голосовой радиосвязи на помощь морзянке пришел новый сигнал. С 1927 г. в качестве сигнала оповещения о бедствии стали использовать троекратно повторенное слово Mayday. В отличие от SOS, слово Mayday является производным от слов естественного языка, хотя его и выбрали прежде всего не поэтому, а потому, что его было легко отличить от других голосовых сигналов и относительно нетрудно распознать даже при плохом качестве связи. Было бы, однако, преждевременно полагать, что речь идет о майском дне. Сигнал происходит от сильно искаженного и переиначенного на английский лад выражение M'aide (помогите мне), встречающееся в некоторых диалектах французского языка. Вы напрасно будете искать его в учебниках или разговорниках для туристов, но есть сведения, что так говорили портовые грузчики на юге Франции. http://polit.ru/science/2006/11/04/sos.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 24-11-2006 05:17 |
|
КНИГА ПО ТЕМЕ Математические досуги Автор: Гарднер М. Издательство: Мир Книга известного американского специалиста в области занимательной математики М. Гарднера в живой и увлекательной форме рассказывает читателю много удивительного из самых разных разделов математики. Любители головоломок смогут испробовать свои силы в решении парадоксов и задач, а те, кто увлекается показом фокусов, - пополнить свой репертуар. Книга доступна самому широкому кругу читателей и доставит много радости всем любителям математических развлечений. http://community.livejournal.com/kniga_file/173543.html Кстати, одна из любимых книг моего детства, при том, что математику я не очень любила. 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 09-12-2006 06:48 |
|
КНИГА ПО ТЕМЕ (Г. А. Гальперин, А. Н. Земляков) Математические бильярды. Рассказывается о поведении бильярдного шара на столе произвольной формы без луз. Описание этого поведения приводит к решению разнообразных вопросов математики и механики: задач о переливании жидкости, об освещении веркальных комнат, об осциллографе и фигурах Лиссажу и др. На доступном школьникам языке вводятся понятия конфигурационного и фазового пространства, понятия геодевических на простейших двумерных поверхностях, предлагаются (с решениями) многочисленные интересные задачи. http://community.livejournal.com/kniga_file/210411.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 15-12-2006 06:06 |
|
КНИГА ПО ТЕМЕ М.Газале. Гномон. От фараонов до фракталов. Мидхат Газале описывает и объясняет свойства гномонов (самоповторяющихся форм), повествует об их долгой и живописной истории, исследует математические и геометрические чудеса, возможные с их помощью. http://community.livejournal.com/kniga_file/222555.html |
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 18-12-2006 12:35 |
|
Арабские цифры 1,2,3,4,5… придумали вовсе не арабы, они пришли к нам из Индии. Просто арабы принесли оттуда эту форму записи чисел, которая потом распространилась через Северную Африку и Испанию в Европу. Истинное преимущество арабских цифр по сравнению с римскими не в их написании, а в гениальном изобретении — позиционной системе счисления, при которой «вес» цифры определяется ее положением. Так, 5 в числе 15 означает всего лишь пятерку, а в числе 2523 — пять сотен (ведь 2523 — это 2 раза по тысяче, 5 раз по сто, 2 раза по десять и 3). http://x-news.ru/index.php?option=com_content&task=view&id=2071&Itemid=2 |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 25-12-2006 02:32 |
|
КНИГА ПО ТЕМЕ Cборник старинных задач, включающий задачи Вавилона, Египта, Греции, Китая, Индии, арабские и русские задачи, а также задачи Западной Европы. Состоит из двух частей: первая - тексты задач, вторая - исторические экскурсы, решения и указания. http://community.livejournal.com/kniga_file/240674.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 02-01-2007 02:44 |
|
В математике есть такое понятие как гугол (googol). Этим забавным словом называют число 1х10100. Записывается оно как единица со ста нулями и может выражаться также как десять дуотригинтиллионов. Слово гугол придумал ребенок – девятилетний племянник математика Эдварда Каснера – в 1920 году. Самое интересное в этом самом гуголе – его абстрактность. Это как бы и не число, потому что с помощью него нельзя ничего сосчитать: не хватит счетных предметов, поскольку количество частиц во всей известной Вселенной меньше, чем гугол. Представили? В бесконечно огромной Вселенной, которую ни перелететь, ни перебежать, не найдется столько атомов и прочей мелкоты, чтобы можно было сказать: тут полный гугол. Не знаю, как вас, а меня такие вещи вводят в ступор. Вы сказки хотели? Ну вот вам сказка. Из одной строчки. Девочка шла по улице и встретила гугол зайцев. Если бы какой-нибудь всемогущий джинн мог воплотить это в реальность, не только на Земле, но и во всей Вселенной наступил бы полный коллапс. Потому что этот гугол зайцев туда просто не поместился бы. Вы еще живы? Тогда представьте себе гуглоугольник. Если начертить правильный многоугольник, количество сторон которого равно гуголу и который по размерам в 1027 раз будет превышать известную нам вселенную, то он всё равно будет выглядеть как круг, даже если его рассматривать в масштабе длины Планка ( = 1,616 × 10−35 м). Начертить такой многоугольник невозможно, потому что во всей вселенной не хватит атомов для изготовления чернил. ПыСы: есть, конечно, еще гуголплекс - гугол в степени гугол. Это число даже записать нельзя - всей бумаги не хватит. Но такое мне уже и представить не под силу... http://melbaa.livejournal.com/64335.html |
|
|
Valerij великий магистр Группа: Администраторы Сообщений: 3753 
|
Добавлено: 10-01-2007 18:45 |
|
Другой практически важной задачей было "честное" распределение земельных наделов. В отличие от современного, Древний Египет был сосредоточен в узкой долине Нила. Ежегодно (вплоть до постройки с помощью СССР Асуанской ГЭС) Нил разливался, сметая все на своем пути. После потопа люди не находили ни заборов, разграничивающих их участки, ни даже построек, но зато земля покрывалась толстым слоем плодородного ила. Поэтому каждый год приходилось заново делить эту плодороднейшую землю. Не случайно с тех пор до Евклида (и много позже) под равенством в геометрии понималось именно равенство по мере (площади, длине, объему). Право делить землю принадлежало жрецам, а нужное для этого знание (умение) являлось их профессиональной тайной, передаваемой от поколения к поколению. Здесь стоит заметить, что циркулей в те времена еще не было. Вместо них египтяне использовали высушенные воловьи хвосты. Герпедонапты (веревковязатели) выравнивали эти эталоны длины между собой, а затем связывали в нужных пропорциях. Например, 3:4:5, что сохранилось в названии египетского треугольника - древнейшего и остроумнейшего способа построения прямого угла. Если у Вас хватило терпения дочитать до этого места длинный, как и сама древняя история, текст, то теперь нужно переварить ключевую мысль: на протяжении первых 33 из 60 веков истории математики в ней не было ни одной теоремы. Более половины своей истории математика оставалась естественной наукой. Геометрия занимала место точно посередине между астрономией и географией, отличаясь от них ничуть не больше, чем сами они между собой. Теоремы и их доказательства - достижение античной цивилизации. Здесь видна прямая связь с государственным устройством - афинской демократией. Только в относительно свободном обществе появилась потребность в доказательствах. Ни фараоны, ни жрецы не нуждались в них. Только уравняв граждан в их правах, демократия сделала возможными как спортивные состязания (олимпийские игры), так и умственные (публичные философские диспуты). http://zhurnal.lib.ru/f/fedotow_w_p/uvvrumdoc.shtml |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 11-01-2007 05:09 |
|
"Puzzle World". На входе довольно большая группа людей, сидя за столами, возятся с различными головоломками. Сразу же приходит детское настроение и хочется внутрь. Внутрь можно пройти бесплатно, потому что поставленные на кассе печати никто не проверяет. Аттракцион состоит из двух частей: налево лабиринт, направо визуальные глюки. Внутри цветастых домиков, изображённых на фотографии, реализованы комнаты, которые напрочь сбивают с толку мозжечок. Вода течёт вверх, качели очень странно раскачиваются, останавливаясь в воздухе там, где останавливаться не должны. Кресло на рельсах, приклееных под углом 45 градусов к стене, вместо того, чтобы катиться вниз, само въезжает наверх. Что касается глюков, то они в основном достаточно известны и основаны на разности контраста, и прочих задуряловах, с которыми нормальный мозг справляется не сразу. http://piterpan.livejournal.com/872348.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 21-01-2007 05:57 |
|
КНИГА ПО ТЕМЕ Занимательные задачи и опыты Автор: Я. И. Перельман Издание 1959 года. В настоящий сборник вошли материалы из разных книг выдающего популяризатора науки Я.И. Перельмана, автором или составителем которых он был. Юный читатель найдет здесь немало интересных опытов и задач из области физики, математики, геометрии и другие научные развлечения. http://community.livejournal.com/kniga_file/254471.html |
|
|
Valerij великий магистр Группа: Администраторы Сообщений: 3753 
|
Добавлено: 24-01-2007 19:55 |
|
69 оптических иллюизий и феноменов - интересный сайт, по названию которого уже понятно, что вы там увидите. Но дело даже не в том, что вы увидите это, а в том, что вам объяснят, как и почему это происходит. Сайт постоянно обновляется. http://www.botinok.co.il/node/21648 |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 25-01-2007 04:50 |
Octavio Ocampo, серия весьма оригинальных рисунков http://yazon.livejournal.com/537422.html 
|
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 10-02-2007 18:39 |
| Китайские цифры http://en.wikipedia.org/wiki/Chinese_number_gestures | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 14-02-2007 04:58 |
|
Картинка. Каждый пиксель на ней получен смещением от предыдущего в зависимости от очередной цифры числа Пи. не видна ли закономерность в миллионе точек? http://sklyarevskiy.livejournal.com/613683.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 08-03-2007 07:35 |
|
Иллюзия, и как ее сделать http://mi3ch.livejournal.com/1040829.html  |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 15-04-2007 06:20 |
|
Довольно большая подборка разных иллюзий http://www.planetperplex.com/en/gallery.html http://mi3ch.livejournal.com/953738.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 18-04-2007 02:30 |
|
Оптические иллюзии Формат: 81 jpg и gif http://community.livejournal.com/kniga_file/366887.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 01-05-2007 06:46 |
|
Корпорация Microsoft объявила о создании новой системы, аналогичной обычному штрихкоду, но содержащей намного больше информации. Сообщается, что нововведение украсит DVD-диски уже в этом году. Как утверждают создатели альтернативной системы под названием "Цветные штрихкоды высокой ёмкости" (High Capacity Color Barcodes — HCCB), с её помощью можно поместить существенно больше информации, чем это позволяет обычный штрихкод. На один квадратный дюйм (примерно 6,5 квадратных сантиметров) HCCB позволяет записать 3,5 тысячи алфавитных символов. Штрихкод представляет собой упорядоченную систему треугольников, окрашенных в разные цвета. Считывать и передавать закодированные данные можно не только с помощью сканеров, но и посредством мобильных телефонов и вебкамер. http://www.membrana.ru/lenta/?7160 |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 18-05-2007 04:18 |
|
Забавный случай на одном из американских форумов. Бурная радость по поводу простейшего арифметического фокуса продолжалась до тех пор, пока забредшая туда ЖЖ-юзерша не высказалась по поводу его элементарности и не усомнилась в том, что автор этого трюка достоин звания "гения". Еще более удивительной оказалась реакция любителей математических фокусов. Вместо того чтобы восхититься математическими способностями azbukivedi они почувствовали себя оскорбленными. http://syndicated.livejournal.com/ljplus_blog/443469.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 19-05-2007 04:19 |
|
Принцип ямы В авральном порядке искал на службе одну затерявшуюся бумажку. Рылся часа полтора. То, что искал, не нашел (она оказалась в портфеле Самого Большого Мужчины в конторе), зато неожиданно нашел другую, не менее важную. Подобные явления природы я называю "принципом ямы". Сформулирован Милном: "- Какой в этом смысл? - спросил Кролик. - Ну, - сказал Пух, - мы все время ищем Дом и не находим его. Вот я и думаю, что если мы будем искать эту Яму, то мы ее обязательно не найдем, потому что тогда мы, может быть, найдем то, чего мы как будто не ищем, а оно может оказаться тем, что мы на самом деле ищем. - Не вижу в этом большого смысла, - сказал Кролик". (с) Кролик не прав. Смысл есть. Этот принцип работает - многократно проверено и лабораторно и в поле. http://burgher.livejournal.com/9109.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 25-05-2007 04:19 |
|
Видите голубые и зелёные спирали? А ведь голубого тут ничего нет. Все спирали одного оттенка зелёного.  Проверка: 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 26-05-2007 04:46 |
|
Иллюзия с Пизанскими башнями, занявшая первое место на конкурсе "Лучшая визуальная иллюзия года ". Из-за особенностей зрительного восприятия нам кажется, что башня на правой картинке наклонена сильнее, хотя обе картинки абсолютно идентичны друг другу. http://billy-red.livejournal.com/354502.html |
|
|
Valerij великий магистр Группа: Администраторы Сообщений: 3753 
|
Добавлено: 30-05-2007 11:53 |
|
Математические чудеса и тайны. http://stepanov.lk.net/gardner/mmm/mmm.html Гексафлексагоны и Другие Математические Развлечения http://stepanov.lk.net/gardner/hex/hex.html Вторая Книга Математических Головоломок и Развлечений журнала "Нучная Америка". http://stepanov.lk.net/gardner/sec/sec.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 04-06-2007 04:34 |
|
Комната Эймса была сконструированная художником и психологом Адельбертом Эймсом в 1946 году. Дальняя стена комнаты расположена не под прямым углом к боковым стенам, как это обычно бывает, а под очень острым углом к одной стене и, соответственно, под тупым углом к другой. Благодаря ложной перспективе, созданной в том числе узорами на стенах и полу (в данном случае - черно-белые клетки), наблюдатель воспринимает эту комнату прямоугольной. В результате оптической иллюзии, человек, стоящий в ближнем (к наблюдателю) углу такой комнаты, выглядит великаном, а находящийся в дальнем углу — карликом. При передвижении человека из одного угла в другой, создается ощущение, что он увеличивается в размерах или уменьшается. Последнее можно наблюдать в следующем видео: http://mi3ch.livejournal.com/1101212.html 
|
|
|
Valerij великий магистр Группа: Администраторы Сообщений: 3753 
|
Добавлено: 16-06-2007 23:34 |
|
Четырёхмерное изображение - реальность? Некоторые утверждают, что мы живём в 3-х мерном мире, наверное, это так. Но вот немного пищи для вашего мозга и как тема для размышлений. На видео показано как рисуется 4-х мерный куб, может ли это быть правдой? Существует ли оранжевая линия там, где она должна быть? Смотрим, думаем, комментируем. Видео http://www.botinok.co.il/node/31772 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 20-06-2007 04:22 |
|
Николай БОГДАНОВ-БЕЛЬСКИЙ (1868 — 1945) Устный счёт. В народной школе С.А.Рачинского 1895, холст, масло, 107х79 см СЕЛЬСКАЯ школа вековой давности. И там на доске задачка: 10 (в квадрате) + 11 (в квадрате) + 12 (в квадрате) + 13 (в квадрате) + 14 (в квадрате) и всё это в числителе, а в знаменателе - 365. И эту задачку решают КРЕСТЬЯНСКИЕ дети... В уме. |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 22-06-2007 03:46 |
| Cтраны, не перешедшие на метрическую систему http://mi3ch.livejournal.com/1116448.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 24-06-2007 04:56 |
|
23 июня 1912 года родился Алан Матисон Тьюринг — английский математик, логик, криптограф, создатель одного из первых компьютеров, основатель теории искусственного интеллекта. Во время Второй Мировой войны Тьюринг работал в Блечли Парке — британском криптографическом центре, где возглавлял одну из пяти групп, Hut 8, занимавшихся в рамках проекта «Ультра» расшифровкой закодированных немецкой шифровальной машиной «Энигма» сообщений Кригсмарине и Люфтваффе. В середине 1940 года он разработал дешифровальную машину «Бомба», позволявшую читать сообщения Люфтваффе. Через полгода удалось взломать и более стойкий шифр Кригсмарине. Позже, к 1943 году, Тьюринг внес ощутимый вклад в создание более совершенной дешифровальной электронно-вычислительной машины «Колосс», использующейся в тех же целях. Благодарное человечество отплатило Тьюрингу гормональной терапией, которая, по сути, была химической кастрацией и привела его к самоубийству на 42 году жизни. Читать об Алане Тьюринге тут: http://old.russ.ru/netcult/20001220.html http://ru.wikipedia.org/wiki/%D0%A2%D1%8C%D1%8E%D1%80%D0%B8%D0%BD%D0%B3 http://community.livejournal.com/ru_history/937216.html |
|
|
Роман великий магистр Группа: Модераторы Сообщений: 1557 
|
Добавлено: 03-07-2007 21:25 |
|
Небольшой математический прикол: Длина земного экватора L = 40 тысяч километров. Ставим по всему экватору на равном расстоянии друг от друга 40 буёв. Сверяем часы. На первом буе вспышка на одну тысячную секунды, затем на втором буе вспышка на одну тысячную секунды и так далее. В результате вспышка совершает полный круг по экватору за время t = 40*0.001 = 0.04 секунды. Инопланетяне видят огонёк, бегающий по Земле со скоростью v = L / t = 40,000/0.04 =1 миллион километров в секунду, что в три с лишним раза больше скорости света, и охреневают. |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 09-07-2007 06:01 |
|
Наткнулся на забавную оптическую иллюзию. Сам анимированный gif прячу под кат из-за двухсот килобайт: Если наблюдать за фигурой девушки в танце, то она несомненно кружится по часовой стрелке. Но стоит на несколько секунд перенаправить взгляд на ее тень отражение в нижней плоскости, как вдруг обнаруживаешь, что она кружится против часовой стрелки. http://neuraum.livejournal.com/127483.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 18-07-2007 06:59 |
|
Но когда дело доходит до штучного исчисления (пуговицы, карандаши, платки, носки и т.д.), то счет идет дюжинами и кратностями всякими. Вот и спрашиваю - почему дюжинами (не седьмицами, например, по дням недели?) Откуда привязка к 12 в счете, если учесть, что такой счет неудобен? Да кто тебе сказал, что он неудобен? Никакой разницы, кроме той, что сидит в голове человека, привыкшего в десятичному счету. Потом - сказали же уже - привязка была изначально к измерениям веса и площади (товарам и земле). А тут двенадцатиричная система куда удобнее. Поскольку позволяет точно взять от принятой единицы не пятую, десятую и половину, а треть, четверть, шестую часть и двенадцатую. Если тебе так легче, представь, что ты взвешиваешь на простых весах-коромыслах сыр (будем считать, что он в один килограмм весом). И у тебя есть единицы измерения - десятичная система ДЫР и двенадцатиричная система БЫР. С соответствующими наборами гирек. Для простоты возьмем, что один ДЫР равен весу сыра и один БЫР тоже ему равен. Соответственно, в обоих системах вес килограммового куска сыра будет равен одной единице - одной большой гире. А теперь подходит покупатель и просит ему отвесить половину. Это ты делаешь с одинаковой легкостью в обоих системах - берешь пять гирек в одну десятую ДЫРА или шесть гирек в одну двенадцатую БЫРА. Но что тебе делать, если покупатель попросит отвесить треть? В двенадцатиричной системе БЫР ты это делаешь с легкостью необычайной - берешь четыре гирьки и дело в шляпе. А в десятичной системе тебе надо отвесить три гирьки, еще три гирьки в одну десятую тех маленьких гирек, еще три в одну десятую уже совсем маленьких гирек... и т.д. Точно отвесить не получится. Аналогично - с одной четвертью. Так какой набор гирь (система мер) удобнее - двенадцатиричная или десятичная, если от одного и того же куска в десятичной ты сможешь точно отмерить только половину, пятую часть, десятую часть и их комбинации, а в двенадцатиричной - половину, треть, четверть, шестую часть, двенадцатую часть и их комбинации? С измерением площадей абсолютно та же история. То есть - как раз в быту двенадцатикратная система удобнее. А 103 гвоздя в двенадцатиричной системе будут "87" гвоздей - никаких сложностей. Только цифры будут какие-нибудь иные, поскольку набор цифр от одного до десяти - это из десятичной системы. Но принцип останется тот же - как "103" означает "десять десятков и еще 3", так "87" будет означать "восемь дюжин и еще 7". В чем разница-то? http://forum.exler.ru/t/117946/p/12721116 |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 20-07-2007 05:28 |
|
Задумывались ли вы, почему 1 - это один? 2 - два? и т.д.? В римских цифрах - это само собой разумеется: количество палочек определяет число. А в арабских? Оказывается - количество углов!  http://forum.exler.ru/t/117946/p/12758819 Опровержение версии: Натянуто вроде, особенно: * загнутый хвостик внизу у 5 * черта в самом низу у 7 * завившийся в спираль хвостик у 9 - ну прям жуть какая-то http://forum.exler.ru/t/117946/p/12763103 |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 22-07-2007 00:34 |
| 12 дюжин составляют Гросс (144). 12 Гроссов - Массу (1728). http://forum.exler.ru/t/117946/p/12779909 | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 06-08-2007 06:16 |
|
Черепа в искусстве http://mi3ch.livejournal.com/1159606.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 15-08-2007 06:25 |
|
Еще об иллюзиях в живописи http://mi3ch.livejournal.com/1162942.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 23-08-2007 02:14 |
|
Вот уже много лет Энди Аарон (Andy Aaron) занимается конструированием весьма специфических калькуляторов. http://www.etoday.ru/2007/08/aaron-adding-machines.php 
|
|
|
Valerij великий магистр Группа: Администраторы Сообщений: 3753 
|
Добавлено: 29-09-2007 02:14 |
|
Трехмерные кошки. Красота! А если интересно как это сделать, то смотрите тут, по-китайски правда, но и так понятно. http://portal.nifty.com/2007/08/15/c/ http://www.botinok.co.il/node/36407 |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 04-11-2007 03:56 |
|
"В невозможном треугольнике каждый угол сам по себе является возможным, но парадокс возникает, когда мы рассматриваем его целиком. Стороны треугольника направлены одновременно и к зрителю, и от него, поэтому отдельные его части не могут образовать реальный трехмерный объект. Ошибки пространственного построения встречались у художников и тысячу лет тому назад. Но первым построившим и проанализировавшим невозможные объекты по праву считается шведский художник Оскар Рейтерсвэрд (Oscar Reutersvard), нарисовавший в 1934 г. первый невозможный треугольник, состоявший из девяти кубиков. (Кстати,заметили,что у него в серединке?) Независимо от Рейтерсвэрда английский математик и физик Роджер Пенроуз повторно открывает невозможный треугольник и публикует его изображение в британском журнале по психологии в 1958 г. В иллюзии использована «ложная перспектива». Иногда такую перспективу называют китайской, так как подобный способ рисования, когда глубина рисунка «двусмысленна», часто встречался в работах китайских художников. Невозможный треугольник Пенроуза С тех пор невозможный треугольник не раз использовался в работах других мастеров. Помимо уже упомянутых можно назвать голландеца М. Эшера, швейцарца Сандро дель Пре (Sandro del Prete), бельгийца Жоса де Мея (Jos de Mey),и венгра Иштвана Ороса (Istvan Orosz). http://samram111.livejournal.com/45641.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 04-11-2007 04:02 |
|
Парадокс Монти Холла — одна из известных задач теории вероятностей, решение которой, на первый взгляд, противоречит здравому смыслу. Задача формулируется как описание гипотетической игры, основанной на американском телешоу «Let’s Make a Deal», и названа в честь ведущего этой передачи. Наиболее распространенная формулировка этой задачи, опубликованная в 1990 году в журнале Parade Magazine, звучит следующим образом: Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трех дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 3, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 1, за которой находится коза. После этого он спрашивает вас, не желаете ли вы изменить свой выбор и выбрать дверь номер 2. Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор? Мэрилин Вос Савант дала свое решение, и на нее обрушились профессора математики со всей Америки. http://kirulya.livejournal.com/1382605.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 06-11-2007 06:04 |
|
Cамое время поразглядывать картинки Стивена Гарднера. Вот,например,феюшки,если Вы думаете,что их тут 4,то совсем даже и нет,их 8,надо только хорошенько всмотреться. "Стивен Гарднер (Steven Michael Gardner), родился в Сан-Диего, Калифорния.И как пишут на сайте очень любит животных, которые окружают его в жизни и являются музами в его живописи." А я думаю,что он просто обладает удивительной способностью видеть в обычном облаке,веточке,цветке - образ,вот он и пытается научить нас этому вИдению. http://samram111.livejournal.com/45955.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 19-11-2007 01:29 |
|
Язык символов йеркиш... Символика сложная, а эстетика вообще инопланетянская (просто «Ангар-18» И бонобо в нем отлично разбираются! http://community.livejournal.com/anthropology_ru/233070.html http://pics.livejournal.com/antimantikora/pic/000w82kf 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 01-12-2007 05:20 |
|
Число пи, которое можно потрогать руками. В музее научного центра Mathematikum в Гиссене. http://drugoi.livejournal.com/2415693.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 25-01-2008 06:50 |
|
Так называемый невозможный треугольник Пенроуза, как и другие «невозможные фигуры», давно будоражит воображение людей: он нередко появляется на картинах художников – таких как Мориц Эшер, а многие энтузиасты пытаются создавать свои трехмерные модели этого объекта (одного такого энтузиаста я даже знаю и имела возможность наблюдать процесс создания «невозможной фигуры» вживую http://melbaa.livejournal.com/111032.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 07-02-2008 03:20 |
|
Оптические иллюзии http://granatik-n.livejournal.com/9930.html http://granatik-n.livejournal.com/10226.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 08-02-2008 05:46 |
|
Иллюзия кривых линий http://sklyarevskiy.livejournal.com/944215.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 10-02-2008 03:15 |
|
Иллюзия хмурых и улыбающихся лиц http://sklyarevskiy.livejournal.com/943798.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 29-07-2008 05:39 |
|
Главный Кафедральный собор Сальты (Аргентина) - смотрите на пол! Отсюда: http://forum.exler.ru/t/136994/p/16256315 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 14-09-2008 03:18 |
|
Два прицепа http://sklyarevskiy.livejournal.com/1111717.html  
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 26-09-2008 07:05 |
|
Про математику и русский А помните, как в школе были присказки-помощники, типа "степка, хочешь щец, фи", или "то-либо-кое-нибудь черточку не забудь", или "цыц, не цыкать, цыган к цыпленочку на цыпочках подходит"? Я до сих пор пользуюсь ими. А вот сейчас почему-то детей такому не учат (или говорят отдельные учителя?). Дело в учителях, видимо. Собственно, я это к чему? Сегодня делали с ребенком деление и вдруг я вспомнила правило (я им тоже вообще-то пользуюсь при случае)- чтобы узнать, делится ли число на три, нужно сложить все цифры этого числа, и если сумма делится, то число делится. Это нам когда-то тоже учитель в школе рассказал, а моим детям не рассказывают. Так вот - кто-нить может объяснить, почему так с делением на три? См. комменты в той теме: http://community.livejournal.com/76_82/3810822.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 02-10-2008 04:23 |
|
Как нарисовать большой и точный овал для крафтовых надобностей. Я сняла на скорую руку картинки, не обижайтесь на качество, главное - принцип понятен Итак, берем лист картона. У меня была большая крышка от коробки с сапогами Определяем, какой в длину будет овал. На этих краях я положила ручку и колпачок от нее В сантиметрах пяти от этих краев втыкаем кнопки ( которые катушечками на концах). Берем толстую нитку или шнурок и обвязываем вокруг кнопок так, чтобы, когда это кольцо натянуто от одной кнопки, сгиб доходил до планируемого края овала. Теперь магия! Вставляем в кольцо карандаш или ручку и начинаем вести, натягивая шнурок... http://rikki-t-tavi.livejournal.com/541240.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 28-10-2008 05:43 |
| Подробности в статье “Как математика поможет в шнуровании ботинок“ http://sklyarevskiy.livejournal.com/1168356.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 11-11-2008 07:31 |
Приглядитесь - ползут по экрану http://sklyarevskiy.livejournal.com/1175250.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 28-11-2008 05:03 |
|
Cперва кажется, что на фото - лицо призрака. однако это иллюзия, на фото чувак держит младенца. Присмотритесь! http://p-i-f.livejournal.com/338804.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 18-01-2009 04:04 |
|
Красота математики http://kirulya.livejournal.com/1798639.html    
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 01-04-2009 05:43 |
|
Cчет нужен. Без него тяжело. Не утащил ли ночью волк барана из отары? Все ли вернулись с охоты? Сколько пальцев на руке? А как трудно вести торговлю! Носильщики носят в трюм корабля мешки с драгоценной корицей и кувшины с добрым эгейским вином. Капитан делает пометки на памятной дощечке: каждый мешок - черточка, каждый десяток - крестик. Римляне придумали цифры: I у них означало единицу, V - пять, Х - десяток, С - сотню. Только сразу и не сообразишь, сколько же это будет: СССLХХVIII? Да и в столбик не сложишь... Привычные нам цифры придумали индусы, а по всему миру распространили их арабские купцы, и с тех пор называются эти цифры арабскими. Правда, писались они вначале не совсем так, как учат тебя в школе. Написание арабских цифр состояло из отрезков прямых линий, где количество углов, соответствовало величине знака. Выглядели они приблизительно так:     Со временем углы сгладились, и цифры приобрели привычный нам вид. Есть там и ноль - цифра без единого угла. Теперь считать стало удобно. Вот уже много столетий весь мир пользуется арабской системой записи чисел. Этими десятью значками можно легко выразить огромные значения. Для подсчета очень больших величин, математики даже придумали удивительное число "гугол" Оно заменяет единицу со ста нулями! http://kirulya.livejournal.com/1977534.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 29-04-2009 04:22 |
|
Про число Эрдеша, наверное, многие слышали. Если вкратце, то оно показывает связь с этим плодовитым венгерским математиком через публикации. У самого Пола Эрдеша это число равно нулю, у любого из его его соавторов - 1, у соавтора соавтора - 2 и т.д. Научные работники могут выявить свое число Эрдеша здесь. В мире кино есть свой аналог: число Бэйкона. Это длина цепочки, связывающей работников киноиндустрии с актером Кевином Бэйконом. Только что прочитал, что есть, оказывается, еще и число Эрдеша-Бэйкона, комбинирующее обе цепочки! Более того, оно вовсе не абстрактно, хотя, конечно, у большинства ученых и актеров стремится к бесконечности. Например, у американского математика Дэйва Байера число Эрдеша-Бэйкона равно 4 или 5, в зависимости от того, как считать одну из публикаций. С Кевином Бэйконом он связан через фильм "A Beautiful Mind", где был консультантом и сыграл небольшую роль. Другой пример: Дэника МакКеллар, игравшая в детстве в сериале "Чудесные годы" и ставшая позже математиком. Ее ЧЭБ равно 6. http://neuraum.livejournal.com/518600.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 03-05-2009 04:54 |
|
Исчезновение Смотрите около 1-2 минут на точку в центре. Вы должны увидеть, как цветные пятна на квадрате начинают пропадать. В итоге, вы увидите чистый квадрат и точку в центре. Явление объясняется усталостью сетчатки глаза. Прекрасная картинка для медитации и симарона: зримо можно представить как исчезает неразрешимая проблема из поля нашего зрения. Остаётся только главное: точка... http://niris.livejournal.com/4236.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 26-05-2009 07:15 |
| Скрытые образы http://p-i-f.livejournal.com/644488.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 29-05-2009 07:02 |
|
Пришла приятная новость для визуалов. Состоялось вручение наград Международного конкурса визуальных иллюзий. Вот сайт, где можно посмотреть представленные на конкурсе работы. - http://illusioncontest.neuralcorrelate.com/ А вот ссылка на иллюзию - победитель - http://illusioncontest.neuralcorrelate.com/2009/the-break-of-the-curveball/ http://astrenata.livejournal.com/317761.html |
|
|
Valerij великий магистр Группа: Администраторы Сообщений: 3753 
|
Добавлено: 04-08-2009 17:48 |
|
Однако, проценты % уклона - это тангенс угла. Таким образом, 100% - это 45o, 30% - это 16.7o, 20% - это 11.3o, 15% - это 8.5o. http://otvet.mail.ru/question/12462917/ |
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 08-08-2009 17:55 |
| А самые помешанные пары женились в 12 часов 34 минуты 56 секунд 7 августа 2009 года, чтобы было уникальное число 1,2,3,4,5,6,7,8,9. | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 05-09-2009 05:01 |
|
Круги и квадраты http://mi3ch.livejournal.com/1590584.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 18-09-2009 06:32 |
|
Римские цифры часто вызывают у нас затруднение. А ведь именно их принято использовать при нумерации столетий и книжных глав, при обозначений размеров одежды и ступеней в музыке. Римские цифры есть в нашей жизни. Так что рано отказываться от них. Проще узнать, понять и выучить. Тем более, что это несложно. Итак, для обозначения цифр в латинском языке приняты комбинации следующих 7 знаков: I(1), V (5), X (10), L (50), C(100), D(500), M (1000). Почему для обозначения цифр 5, 50, 100, 500 и 1000 были выбраны латинские буквы? Оказывается, это не латинские буквы, а совсем иные знаки. Дело в том, что основой для латинского алфавита, (а он, кстати, существует в нескольких вариантах - 23, 24 и 25 буквы) послужил западногреческий алфавит. Таким образом, к западногреческому алфавиту восходят три знака L, C, и M. Здесь они обозначали придыхательные звуки, которых не было в латинском языке. Когда оформлялся латинский алфавит, именно они оказались лишними. И их приспособили для обозначения чисел в латинской графике. Позднее они по написанию совпали с латинскими буквами. Так, знак С (100) стал похож на первую букву латинского слова centum (сто), а М - (1000) - на первую букву слова mille (тысяча). Что же касается знака D (500), то он представлял собой половину знака Ф (1000), а потом уже стал похож на латинскую букву. Знак V (5) являлся всего-навсего верхней половиной знака Х (10). В связи с этим, кстати, популярная теория о том, что название церковной должности Папы Римского (Vicarius Filii Dei) при замене букв римскими цифрами в сумме дает “дьяволово число”, кажется забавной. Итак, как же разобраться в латинских числах? Если знак, обозначающий меньшее число, стоит справа от знака, обозначающего большее число, то меньшее прибавляют к большему; если слева - то вычитают: VI - 6, т.е. 5+1 IV - 4, т.е. 5-1 LX - 60, т.е. 50+10 XL - 40, т.е. 50-10 CX - 110, т.е.100+10 XC - 90, т.е. 100-10 MDCCCXII - 1812, т.е. 1000+500+100+100+100+10+1+1. Возможно различное обозначение одного и того же числа. Так, число 80 можно представить как LXXX (50+10+10+10) и как XXC(100-20). Основные римские цифры выглядят так: I(1) - unus (унус) II(2) - duo (дуо) III(3) - tres (трэс) IV(4) - quattuor (кваттуор) V(5) - quinque (квинквэ) VI(6) - sex (сэкс) VII (7) - septem (сэптэм) VIII (8) - octo (окто) IX (9) - novem (новэм) X (10) - decem (дэцем) и т.д. XX (20) - viginti (вигинти) XXI (21) - unus et viginti или viginti unus XXII (22) - duo et viginti или viginti duo и т.д. XXVIII (28) - duodetriginta (дуодэтригинта) XXIX (29) - undetriginta (ундэтригинта) XXX (30) - triginta (тригинта) XL (40) - quadraginta (квадрагинта) L (50) - quinquaginta (квинквагинта) LX (60) - sexaginta (сэксагинта) LXX (70) - septuaginta (сэптуагинта) LXXX (80) - octoginta (октогинтна) XC (90) - nonaginta (нонагинта) C (100) - centum (центум) CC (200) - ducenti (дуценти) CCC (300) - trecenti (трэценти) CD (400) - quadrigenti (квадригэнти) D (500) - quingenti (квингэнти) DC (600) - sexcenti (сэксценти) DCC (700) - septigenti (сэптигэнти) DCCC(800) - octingenti (октигенти) CM (DCCCC) (900) - nongenti (нонгэнти) M (1000) - mille (милле) MM (2000) - duo milia (дуо милиа) V (5000) - quinque milia (квинквэ милиа) X (10000) - decem milia (дэцем милиа) XX (20000) - viginti milia (вигинти милиа) C (1000000) - centum milia (центум милиа) XI (1000000) - decies centena milia (дэциэс центэна милиа)" http://p-i-f.livejournal.com/807028.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 23-09-2009 08:13 |
|
Тессеракт (от др.-греч. четыре луча) — четырёхмерный гиперкуб — аналог куба в четырёхмерном пространстве. Изображение является проекцией (перспективой) четырёхмерного куба на трёхмерное пространство. Согласно Оксфордскому словарю, слово «tesseract» было придумано и начало использоваться в 1888 Чарльзом Говардом Хинтоном (1853—1907) в его книге «Новая эра мысли». Позже некоторые люди назвали ту же самую фигуру «тетракубом». Стереопара тессеракта изображается как две проекции на трёхмерное пространство. Такое изображение тессеракта разрабатывалось с целью представить глубину, как четвёртое измерение. Стереопара рассматривается так, чтобы каждый глаз видел только одно из этих изображений, возникает стереоскопическая картина, воспроизводящая глубину тессеракта. Тессеракт в искусстве У Эдвине А. «Новая Равнина Абботта», гиперкуб выступает рассказчиком. В одном эпизоде «Приключений Джимми Нейтрона»: «Мальчик-гений» Джимми изобретает четырёхмерный гиперкуб, идентичный фолдбоксу из романа «Дорога славы» 1963 Хайнлайна. Роберт Э. Хайнлайн упоминал гиперкубы, по крайней мере, в трёх научно-фантастических рассказах. В «Дом четырех измерений» («Дом, который построил Тил») (1940) он описал дом, построенный как развёртка тессеракта. В романе «Дорога славы» Хайнлайна описана гиперразмерная посуда, которая была изнутри больше, чем снаружи. Рассказ Генри Каттнера «Mimsy Were the Borogoves» описывает развивающую игрушку для детей из далёкого будущего, по строению похожую на тессеракт. В романе Алекса Гарленда (1999), термин «тессеракт» используется для трехмерной развёртки четырёхмерного гиперкуба, а не гиперкуба непосредственно. Это метафора, призванная показать, что познающая система должна быть шире познаваемой. Сюжет фильма «Куб 2: Гиперкуб» сосредотачивается на восьми незнакомцах, пойманных в ловушку в «гиперкубе», или сети связанных кубов. Телесериал «Андромеда» использует тессеракт-генераторы как устройство заговора. Они прежде всего предназначены, чтобы управлять пространством и временем. Картина «Распятие на кресте» (Corpus Hypercubus) Сальвадора Дали (1954) Комиксы «Nextwave comic book» изображают средство передвижения, включающее в себя 5 зон тессеракта. В альбоме Voivod Nothingface одна из композиций названа «В моём гиперкубе». В романе Энтони Пирса «Маршрут Куба» одна из орбитальных лун Международной ассоциации развития называется тессерактом, который был сжат в 3 измерения. В сериале «Школа „Чёрная дыра“» в третьем сезоне есть серия «Тессеракт». Лукас нажимает на секретную кнопку и школа начинает складываться как математический тессеракт. Термин «тессеракт» и производный от него термин «тессировать» встречается в повести Мадлен Л’Энгл «Складка времени» http://p-i-f.livejournal.com/810659.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 02-10-2009 03:49 |
|
«Делить на ноль нельзя!» — большинство школьников заучивает это правило наизусть, не задаваясь вопросами. Все дети знают, что такое «нельзя» и что будет, если в ответ на него спросить: «Почему?» А ведь на самом деле очень интересно и важно знать, почему же нельзя. Всё дело в том, что четыре действия арифметики — сложение, вычитание, умножение и деление — на самом деле неравноправны. Математики признают полноценными только два из них — сложение и умножение. Эти операции и их свойства включаются в само определение понятия числа. Все остальные действия строятся тем или иным образом из этих двух. Рассмотрим, например, вычитание. Что значит 5 – 3? Школьник ответит на это просто: надо взять пять предметов, отнять (убрать) три из них и посмотреть, сколько останется. Но вот математики смотрят на эту задачу совсем по-другому. Нет никакого вычитания, есть только сложение. Поэтому запись 5 – 3 означает такое число, которое при сложении с числом 3 даст число 5. То есть 5 – 3 — это просто сокращенная запись уравнения: x + 3 = 5. В этом уравнении нет никакого вычитания. Есть только задача — найти подходящее число. Точно так же обстоит дело с умножением и делением. Запись 8 : 4 можно понимать как результат разделения восьми предметов по четырем равным кучкам. Но в действительности это просто сокращенная форма записи уравнения 4 · x = 8. Вот тут-то и становится ясно, почему нельзя (а точнее невозможно) делить на ноль. Запись 5 : 0 — это сокращение от 0 · x = 5. То есть это задание найти такое число, которое при умножении на 0 даст 5. Но мы знаем, что при умножении на 0 всегда получается 0. Это неотъемлемое свойство нуля, строго говоря, часть его определения. Такого числа, которое при умножении на 0 даст что-то кроме нуля, просто не существует. То есть наша задача не имеет решения. (Да, такое бывает, не у всякой задачи есть решение.) А значит, записи 5 : 0 не соответствует никакого конкретного числа, и она просто ничего не обозначает и потому не имеет смысла. Бессмысленность этой записи кратко выражают, говоря, что на ноль делить нельзя. Самые внимательные читатели в этом месте непременно спросят: а можно ли ноль делить на ноль? В самом деле, ведь уравнение 0 · x = 0 благополучно решается. Например, можно взять x = 0, и тогда получаем 0 · 0 = 0. Выходит, 0 : 0 = 0? Но не будем спешить. Попробуем взять x = 1. Получим 0 · 1 = 0. Правильно? Значит, 0 : 0 = 1? Но ведь так можно взять любое число и получить 0 : 0 = 5, 0 : 0 = 317 и т. д. Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них. То есть мы не можем сказать, какому числу соответствует запись 0 : 0. А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла. Выходит, что на ноль нельзя делить даже ноль. (В математическом анализе бывают случаи, когда благодаря дополнительным условиям задачи можно отдать предпочтение одному из возможных вариантов решения уравнения 0 · x = 0; в таких случаях математики говорят о «раскрытии неопределенности», но в арифметике таких случаев не встречается.) Вот такая особенность есть у операции деления. А точнее — у операции умножения и связанного с ней числа ноль. Ну, а самые дотошные, дочитав до этого места, могут спросить: почему так получается, что делить на ноль нельзя, а вычитать ноль можно? В некотором смысле, именно с этого вопроса и начинается настоящая математика. Ответить на него можно только познакомившись с формальными математическими определениями числовых множеств и операций над ними. Это не так уж сложно, но почему-то не изучается в школе. Зато на лекциях по математике в университете вас в первую очередь будут учить именно этому. http://bertalda.livejournal.com/123137.html |
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 25-10-2009 13:44 |
|
Я тогда же вспомнил задачку про лгунов и рыцарей, но, видимо, не к месту. А потом вообще вспомнил сколько удовольствия в свое время (лет в 11) мне доставили такие задачки. Их много есть в книге Рэймонда Смаллиана "Алиса в стране смекалки". Например Представьте себе, что перед вами двое совершенно неотличимых близнецов. Один всегда лжет, другой всегда говорит правду. Одного из них зовут Джон. Предположим, что вам встретились близнецы и вы хотите узнать, кто из них Джон. Каждому из них вам разрешается задать только один вопрос, на который можно ответить односложно: "да" или "нет". Сам вопрос должен состоять из трех слов. Какой вопрос вы задали бы? И, чуть-чуть поискав в сети, я нашел нормальную электронную версию книги. Вот она. http://dirty.ru/comments/260570/#new |
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 25-11-2009 12:24 |
|
О самоуверенном авторе задачек про бегунов Вам не предлагали решить четыре задачки, две из которых - про бегунов? Если Вас выставляли "слабым звеном", то давайте ответим взаимностью автору. Приведу текст задачек, чтобы не быть голословным. Вы можете их найти в Интернета в большом количестве копий, если зададите в поисковой системе запрос вроде "Вы обогнали последнего бегуна 4100". Вот один из вариантов текста: http://www.plisco.ru/notes/physmath/opinionated.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 30-11-2009 03:02 |
| Приколы на тему оптических иллюзий http://vasily-sergeev.livejournal.com/1149930.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 01-12-2009 04:21 |
|
Все ромбы на листе одинаковые, отдельный ромб тоже такой же. У каждого ромба нижняя часть темнее и плавно переходит в более светлую верхнюю часть. Соседство темного со светлым создает иллюзию того, что каждый ромб темнее своих нижних соседей. Вот, нагуглил подробности: http://en.wikipedia.org/wiki/Same_color_illusion http://mi3ch.livejournal.com/1639685.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 08-01-2010 07:32 |
|
Гарзай разговаривает по телефону на пушту с пакистанцем, живущим в России. Вдруг слышу русский. - ... тридцать два, пятьдесят, сорок восемь... - ??? У пуштунов что, названий цифр своих нет???? - Ну почему, есть. Просто в разговоре сложно различить, поэтому часто называем цифры на другом языке, известном говорящим: фарси, англйиском, голландском или вот русском... А то путаница потом http://amina-kosha.livejournal.com/129174.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 07-04-2010 03:15 |
Это не спираль http://nickfriend.livejournal.com/324001.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 09-04-2010 06:47 |
|
Эти иллюзии изобрел японский психиатр Акиоши Китаока. Врач утверждает, что иллюзии фактически неподвижны для спокойного, уравновешенного, отдохнувшего человека. Если иллюзии активно движутся - вам нужен отдых. Ну, а если иллюзии движутся очень быстро - вам нужно обратиться в больницу, лучше сразу в психиатрическую. Быстрое движение иллюзии обычно наблюдается у маньяков. http://users.livejournal.com/tasja_/217379.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 12-04-2010 01:42 |
| До и после свадьбы: картинки-перевертыши http://marinni.livejournal.com/466274.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 06-05-2010 03:21 |
| Шаровой мир Джорджа Харта http://mi-cha-el.livejournal.com/246663.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 09-05-2010 04:39 |
|
Перед вами два изображения Пизанской падающей башни, но обе фотографии абсолютно одинаковы, т.е. это один и тот же снимок. Тем не менее, кажется, что правая башня наклонена больше, как будто сфотографирована с другой точки. Иллюзия заключается в том, что наш мозг воспринимает две картинки так, как если бы они были частью одного целого. Так можно и совсем завалиться : Иллюзия хорошо работает также и с другими сценами, такими как, дороги или железнодорожные пути, уходящие за горизонт. Все изображения абсолютно одинаковы http://p-i-f.livejournal.com/1334632.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 10-05-2010 05:09 |
| Лабиринт "Морская болезнь" http://maraz-m-moroz.livejournal.com/308119.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 02-07-2010 05:45 |
| Оптические иллюзии на любой вкус http://vitaowly.livejournal.com/8193.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 01-09-2010 07:58 |
| Парадокс Монти Холла http://p-i-f.livejournal.com/1650551.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 04-09-2010 04:44 |
|
Наткнулся на хороший магический квадрат Ли Саллоуса - кошмар археолога Черепки собираются в целую тарелку по строкам, столбцам и по диагонали http://mi3ch.livejournal.com/1777555.html 
|
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 24-09-2010 04:53 |
| Анаморфозы. Зашифрованные изображения и зеркала. История http://marinni.livejournal.com/596950.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 11-10-2010 05:02 |
|
Итак, собеседование. Проверили старшего - о, да в класс А, младшего сразу вся комиссия - что проверять - такой похожий на маму и на дедушку, кто может сомневаться, сразу запишем. Нет, сказала председатель комиссии - хочу спросить лично. Взяла листок и написала 68 и спросила - Мальчик, а какую цифру я написала? Мальчик, сын и внук учителей математики, посмотрел на даму и ответил: - Вы написали число шестьдесят восемь, которое состоит из двух цифр - шестерки, которое показывает десятки и восьмерки, которое показывает сколько единиц. Тишина... Больше никто ничего не пытался узнать,записали в 1 класс Запоминаем - цифры - это значки (как буквы) А мы имеем дело с числами (числа - это как слова) http://hanima.livejournal.com/355354.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 01-11-2010 02:23 |
|
Оптические иллюзии встречаются на самых неожиданных произведениях искусства. Например, на каждой из этих 30 старинных гравюр спрятан некий жутковатый образ. Чтобы его увидеть, нужно чуть отдалиться от монитора. Если все-таки не увидели — подсказка на последней картинке. http://vasily-sergeev.livejournal.com/1830393.html |
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 06-12-2010 12:30 |
|
Итак, этот карточный трюк изобретён американским математиком Мартином Краскалом и впервые опубликован в 1975 году. Перетасуйте колоду из 52 карт (без джокеров) и разложите рядами по девять карт, как показано на картинке. Предложите любому из присутствующих загадать карту в верхнем ряду, а затем, согласно номиналу карты (тузы считаем за единицы, все остальные картинки - за пятёрки), сделать соответствующее количество шагов вправо, переходя в начало следующего ряда при необходимости. Пусть он пройдёт таким образом всю колоду, согласно значениям карт, на которых выполняются остановки. А теперь удивите присутствующих, сообщив, на какой из карт он остановился! Для этого про себя выполните процедуру, описанную выше, также выбрав любую карту из верхнего ряда. Кстати на сайте, откуда взята картинка, колода тасуется при каждом обновлении страницы. Данный трюк интересен тем, что основывается не на ловкости рук, а на статистической закономерности. Вероятность угадывания превышает 85%, если вы выбираете первую карту. Поэтому будьте готовы и к редким неудачам. А еще принцип Краскала нашёл применение также и в алгоритмах поиска, в том числе, при решении задачи дискретного логарифмирования. http://dirty.ru/comments/297227/#new |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 08-12-2010 04:42 |
|
Митсумаса Анно - известный японский иллюстратор и автор детских книг. Однажды он бросил преподавать детям математику и уехал в Париж учиться живописи. А потом стал иллюстрировать детские книги. Любовь к математике привела его к тому, что он придумал и нарисовал несколько книг, где " не уча" учит детей математическому мышлению. Там такие вещи, которые не связаны напрямую с простым счетом, их увлекательно рассматривать и разгадывать, отвечать на вопросы и наблюдать в жизни. http://rikki-t-tavi.livejournal.com/803345.html |
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 12-12-2010 18:05 |
|
В 1910 году парень из Флориды Клиффорд Адамс увидел в местной газете задачку: нужно было расположить числа от 1 до 19 в клетки шестиугольника со стороной три так, чтобы их суммы по любым прямым линиям была равны, - другими словами, нужно было найти магический гексагон. Не имея специального образования Адамс начал искать решение перебором, используя набор из керамических плиток с числами. Всё свободное от работы грузчиком время он отдавал поиску, который продолжался сорок семь лет. Наконец, в 1957 году он нашёл решение и записал его второпях на клочке бумаги, который тут же... потерял. В попытках воспроизвести решение прошло ещё пять лет. В декабре 1962 года нашлась та самая бумажка. И да, Адамс нашёл первый известный магический гексагон. Кроме того, оказалось, что этот гексагон является вообще единственным нормальным магическим из всех любого размера. По моим подсчётам с учётом симметрии у Адамса было более трёхсот триллионов вариантов, и без везения тут не обошлось. http://dirty.ru/comments/297533/#new |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 15-12-2010 04:59 |
|
Еще две книги Митсумасы Анно - "Математические игры-2" и "Загадочный умножательный горшок Анно" http://rikki-t-tavi.livejournal.com/806029.html |
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 02-01-2011 17:39 |
|
Итак, сейчас нас 33.333 человека. Страшно подумать, но если все пользователи Dirty вдруг решат сообразить на троих, то получится R5пьяных компаний. О чем это я? Да, это всего лишь число одиннадцать тысяч сто одиннадцать, но это число относится к семейке, свойства которой столь интересны, что такие числа получили свое собственное название - репьюниты, и обозначение Rn для числа из n единиц. Здесь немного про связь репьюнитов с простыми дробями и про Иоганна Бернулли, развлекавшегося разложением репьюнитов на простые множители. Что характерно, разлагаются почти все, на текущий момент известно только девять репьюнитов, являющихся простыми числами. Кроме того, если к числу прибавить сумму его цифр, то получится (сюрприз!) другое число. Исходное число в данном случае называется генератором, а получившееся - порожденным. Если у числа нет генераторов - оно называется самопорожденным. Так, о чем это я? Да! Если записать 33333 два раза подряд, то получится самопорожденное число 3333333333. Это "ЗЗЗЗЗЗЗЗЗЗ..." неспроста! В общем, почтенная публика может почитать ссылки, а математиков приглашаю в комментарии развлечься занимательной нумерологией. http://dirty.ru/comments/297230/#new |
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 16-01-2011 20:30 |
|
Задумайте (почти) любое число от 0 до 9999. Задумали? Теперь идём на этот сайт и ищем это число. http://www2.stetson.edu/~efriedma/numbers.html http://dirty.ru/comments/301484/#new |
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 20-01-2011 19:01 |
|
Впервые эта техника была применена великим Леонардо да Винчи в 1485 году (eng.). Суть ее состоит в следующем: вы видите перед собой изображение, которое, на первый взгляд, не имеет никакого смысла, однако, в результате оптического смещения, это изображение складывается в легко прочитываемый образ. Пик популярности анаморфоз приобрел в XVI – XVIII веках. Наиболее известная работа того времени принадлежит кисти Ганса Гольбейна младшего и называется «Послы» (при определенном угле обзора можно увидеть череп). В наше время анаморфоз вы можете встретить как на улице, в работах Курта Веннера, так и в традиционном искусстве, в работах Иштвана Ороса. http://dirty.ru/comments/301756/#new |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 26-01-2011 03:41 |
| Фантастические абстрактные фракталы http://affinity4you.livejournal.com/782081.html | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 29-01-2011 09:35 |
|
Есть такая удивительная и вроде бы даже бредовая вещь как – запрещенные числа. Вы наверняка знакомы с повседневными числами 7, 15, 42, Пи, сто пятьдесят миллионов и гуглоплекс. Но задумывались ли вы, что наряду с этими обычными числами, существуют так же необычные, числа запрещенные к публикации? Числа за хранение, распространение и употребление которых может наступить юридическая ответственность вплоть до тюрьмы. Бред, правда? На ум сразу приходят всякие “сатанинские” 13 и 666, но запрет в данном случае отнюдь не по религиозным причинам. Вот пример запрещенного числа: http://p-i-f.livejournal.com/1991731.html |
|
|
DOMINIC великий магистр Группа: Участники Сообщений: 560 
|
Добавлено: 10-02-2011 16:53 |
| Прикольные фото, основанные на масштабных иллюзиях http://www.blogbaster.org/post133699302/?upd | |
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 12-02-2011 04:28 |
|
А Вы заметили, что сегодняшний день является палиндромом? 11022011 - Дата сегодня в этом виде читается в обе стороны одинаково :) Сегодня необычный день! http://zanderlv.livejournal.com/105643.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 16-02-2011 04:13 |
|
Руководство АБФФ, разобравшись в тонкостях экстремистской нумерологии, рекомендовало футбольным клубам избегать на майках футболистов определенных цифр, в которых может быть усмотрена экстремистская подоплека. так сообщает издание "Прессбол", в эту категорию попали игровые номера 14, 18, 28, 88. При этом авторы рекомендаций ссылаются на некий регламент ФИФА, который, возможно, восприняли слишком буквально. Поясним, что 14/88 - это кодовый лозунг, также употребляющийся в качестве приветствия или подписи у белых националистов. Число 18 используется неонацистами для обозначения дня рождения Адольфа Гитлера, а 28 - зашифровка латинских букв BH - аббревиатуры одной из самых влиятельных в мире ультраправых организаций "Blood&Honour". (www.mixnews.lv/ru/sports/news/2011-02-03/57591) да давайте запретим еще номер 1, так как напоминат кол на который Иван Грозный сажал непокорных, номер 7 потому, что напоминает топор которым рубили головы, и номер 69 потому, что так в простонародье называют позу в сексе и нех тут пропагандировать секс! может мне еще не отмечать свой день рождения потому, что в этот день в 1939 году Гитлер напал на Польшу и развязал Вторую мировую войну? http://roninn.livejournal.com/305994.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 14-03-2011 02:24 |
|
Болгарский сотовый оператор Mobitel заморозил «блатной» номер после того, как за последние 10 лет умерли все абоненты, получившие его. Это номер 0888 888 888, пишет Daily Telegraph. Звонящие на него слышат, что «номер недоступен». Официально в компании эту информацию не комментируют. В 2001 году скончался первый владелец этого номера — бывший топменеджер Владимир Грашнов. Он умер от рака в возрасте 48 лет, и ходили слухи, что конкуренты подвергли его смертельной дозе радиоактивного облучения. Затем этот номер перешел к «крестному отцу» болгарской мафии Константину Димитрову, которого застрелили в 2003 году в Нидерландах в ресторане на глаза. Ему был 31 год. В этом убийстве подозревают русскую мафию. Потом этот номер перешел к бизнесмену Константину Дишлиеву Бушелеву, которого застрелили в Софии в 2005 году. С тех пор номер никому не передавали, поскольку по факту убийства Дишлиева велось расследование. После смены руководства Mobitel было принято решение не использовать этот номер вовсе. http://wombatik.livejournal.com/3317366.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 15-05-2011 05:01 |
|
Загадочная цифра"7" и циклы старинных гравюр. Семь чудес света-продолжение. Семь богов удачи. У меня уже много постов с циклами гравюр с числом "7". Но после вчерашнего совпадения решила собрать все примеры http://marinni.livejournal.com/711260.html |
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 01-06-2011 17:25 |
|
Под воздействием звука, давления звуковых волн и вибраций, беспорядочная россыпь песка на листе стекла или другой пластине начинает выстраиваться в точные геометрические орнаменты. Причем, форма рисунка напрямую зависит от частоты звука. Такие фигуры называются фигурами Хладни. В своих экспериментах Эрнст Ф. Хладни насыпал мелкий песок на стеклянную пластинку. Затем он проводил смычком по ребру пластинки, вызывая колебания. Песок отскакивал от вибрирующих областей и собирался в узлах, точках, остававшихся неподвижными. Через несколько секунд пластинка покрывалась рядом песчаных кривых. Конфигурация рисунка была симметричной и весьма эффектной - она состояла из звёзд и других геометрических фигур. Общий рисунок зависел от формы пластины, положения опор и частоты вибрации. http://dirty.ru/comments/313836/#new |
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 02-08-2011 17:44 |
|
Как впихнуть всего побольше в ограниченный объем? В математике, это называется задача об упаковке. Задачу о максимально плотной упаковке шаров геометры решали с древности. Кеплер предположил, что пирамида шаров есть эта упаковка, ее плотность 0.74048. А доказательство этого было получено недавно. Thomas Hales (род. в 1958 году) объявил в 1998 об этом доказательстве, и четыре года эксперты не могли ни принять его результат, ни опровергнуть, наконец решили что скорее всего (на 99 процентов) решение правильно. Доказательство занимает 100 страниц теории плюс результаты немаленькой комьютерной программы, которая перебирает варианты и отбрасывает один за одним. Интересна и связанная задача: Kissing numbers – целующиеся числа – это число соседей – упакованных сфер, соприкасяющихся с одной данной. На плоскости это число равно шести, а в трехмерном пространстве - 12 (правильный ответ предположил еще Ньютон, а вроде доказан он был в конце 19 века, и только в 1956 году поставили последнюю точку). А как насчет упаковки эллипсоидов? Можно конечно просто растянуть шары, изменив масштаб в одном направлении. Но есть и лучшее решение, его нашли недавно, (Sloane 1998). Фокус в том чтобы укладывать слои поперек предыдущих. Оптимально оно или нет, пока неизвестно. Ресультат был подтвержден экспериментально, на конфетах (Принстон, 2004). Можно изучать упаковки икосаэдров, бубликов–торов и других тел (Nature, 2009), задачи имеют прямое отношение к поликристаллам и пока не решены. Другая интересная задача – наименее плотная упаковка сфер, которая все же не дает им рассыпаться, или порог, до которого сферы могут держаться друг за друга или застревать (jamming). Удивительно, что нужно то всего 0.0555. обьема. Эта задача моделирует переход в клисталлическое состояние из газа, аслучайная упаковка моделирует сыпучие тела. Напоследок, вот альбом интересных упаковочных задач Эрика Фридмана (Erich Friedman), решенных меньше чем месяц назад: Как вписать данное число кругов в прямоугольник данного периметра, чтобы максимизировать сумму длин их окружностей. Там же масса других задачек на плоскости. http://dirty.ru/comments/319430/#new |
|
|
Роман великий магистр Группа: Модераторы Сообщений: 1557 
|
Добавлено: 19-08-2011 20:25 |
|
Лица Чернова (англ. Chernoff faces) - отображение многомерных данных в виде человеческого лица, его отдельных частей. Люди легко распознают лица и без затруднения воспринимают небольшие изменения в нем. Американский математик Герман Чернов в 1973 году опубликовал работу, в которой изложил концепцию использования этой способности восприятия лица человека для построения пиктографиков. Их применяют, как правило, в двух случаях: 1) когда нужно выявить характерные зависимости или группы наблюдений и 2) когда необходимо исследовать предположительно сложные взаимосвязи между несколькими переменными. Лица Чернова являются одним из самых эффективных способов визуализации многомерных данных, и позволяет легко оценивать одновременно большое их количество. http://ru.wikipedia.org/wiki/%CB%E8%F6%E0_%D7%E5%F0%ED%EE%E2%E0 |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 29-08-2011 05:59 |
|
Художники и геометры играли с покрытиями (мозаиками) с древности. Одинаковые куски – шестигранные соты или параллелограммы – ложатся на плоскость, покрывая ее всю, причем картина бесконечно повторяется. Гоогле дает тысячи картинок в ответ на «plane tessellation», например, это. Имеется 17 типов симметрии, которые показаны здесь. Эшер (1902–1972) открыл потенциал покрытий в живописи, и здесь галерея его работ по симметрии. B 1974 году представления о покрытиях изменились: Пенроуз (sir Roger Penrose, Oxford) нашел способ покрыть всю плоскость двумя ромбами (Penrose tiling, обратите внимание на картинку). Поразительно, что это покрытие непериодично! Бесконечно похожая на себя, но не повторяющаяся мозаика вызывает легкий шок; непонятно, порядок это или хаос. Оказалось, и то и другое. Мозаика Пенроуза – квазикристалл. Это означает, что стартуя с небольшого количества ромбов и соблюдая несколько правил добавления новых, мы всегда получим одну и ту же мозаику (нет никакой свободы выбора, как и в периодических структурах). Оказалось, что мозаика получается как сечение пятимерной кубической решетки наклонной плоскостью. Она наследует и порядок кубов и беспорядок линий пересечения. Потом нашли много других таких покрытий (здесь Hirschhorn Tile – непериодическое покрытие одним пятиугольником). Разумеется, выяснилось, что средневековые мусульмане их тоже знали (кажется, они знали массу всего о симметриях, но к сожалению, это не получило развития). Из покрытий Пенроуза иногда делают мозаики на стенах и на полу. (Здесь Пенроуз стоит на своей мозаике), а здесь Мельбурн. Жаль, Эшер не дожил! По мудрому замечанию Я.Б.Зельдовича, «Все, что придумали математики, рано или поздно будет реализовано физиками». Через два года после открытия Пенроуза, Шехтман и соавторы синтезировали первые квазикристаллы – физические квазипериодические объекты, и с этих пор над ними многие активно работают, ибо они обладают повышенной прочностью, низким трением, замечательной дифракционной картиной, и другими интересными свойствами. В 2010 на Камчатке нашли природные квазикристаллы. Вернемся к геометрии. Казалось бы, что нового можно увидеть в планиметрии после того, как математики вглядывались в нее 2,5 тысячи лет со времен Евклида? Одкако, нашлось принципиальное развитие, соединившее порядок и беспорядок, и безумно красивое само по себе! http://sklyarevskiy.livejournal.com/2797042.html |
|
|
Фон-Барон великий магистр Группа: Участники Сообщений: 3391 
|
Добавлено: 06-09-2011 17:00 |
|
Перед вами шедевр Эшера "Галерея гравюр" ( M.C. Escher, "Print Gallery",1956). Видите дырку в центре? Эшер написал, что не может закончить эту картину и оставляет ее. Поклонники и искусствоведы гадали, почему бы? Среди версий были: предсказанная "черная дыра", инь и янь, дуализм волн и частиц, и масса другого всякого. Загадку разгадал математик професор Ленстра (H. W. Lenstra) около 2000. Он понял, каким образом Эшер искажает пространство на картине: Если разделить картину на маленькие квадраты, то каждый квадрат изменяет свой размер и поворачивается по определенному закону (конформное преобразование); обратное искажение восстанавливает реалистический городской пейзаж. Получив формулу, Ленстра продолжил это преобразование, и обнаружил что на месте дырки должна быть та же картина, но уменьшенная и повернутая, естественно с уменьшенной дыркой посередине, в которой ... можно не продолжать? Спираль накручивает виток за витком, картина в картине в картине... Здесь хорошая страница об этой истории, здесь видео–клип превращения, а здесь относительно популярная статья Ленстры о математике преобразования; в 2007 вышел отличный фильм Achieving the Unachievable (Достижение недостижимого), директор – Jean Bergeron. http://dirty.ru/comments/318754/#new |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 18-10-2011 06:41 |
|
У каждого из нас, наверное, есть любимое число или числа. Кто-то из называет счастливыми. Я вот всегда предпочитала нечетные числа чётным. Уж и не знаю почему. И еще всегда любила число 11. Ну, тут понятно, день рождения у меня одиннадцатого. В этом году, для тех кто следит, есть два чудесных дня. 1.11.11 и 11.11.11. Ну, круче было бы, конечно, если б и год был полностью единический, 1111, а так приходится за уши притягивать и не обращать внимания на первые цифры года. А еще в этом году, по вполне понятной логике, если вы к двум последним цифрам года своего рождения прибавите то, сколько вам в этом году исполнилось /исполнится лет, то получится 111. Ну, или для малышей 21 века 11. Вот как смешно. так что кругом единички. Надо бы как-то отметить этот день, 11 ноября. http://zagrebchanka.livejournal.com/244597.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 26-12-2011 08:20 |
|
Крупнейшая европейская страховая компания "Акса" обнаружила своеобразную закономерность, связанную с нумерацией квартир и частотой возникающих с ними проблем. Согласно проведенному ее специалистами анализу, наибольшее количество пожаров, наводнений и ограблений происходит в квартирах, имеющих номер 33. При этом в квартирах под номером 76 количество подобных происшествий минимально по сравнению с любыми другими. Между тем среди европейского населения сохраняется предубеждение относительно цифры 13. Каждый восьмой человек отказывается въезжать в квартиру под данным номером. А повышенной симпатией пользуется номер 7. "Мы пришли к заключению, что наиболее "проблемные" квартиры находятся в номерном отрезке 31 - 40, а наиболее "спокойные" - 71 - 80", заявил одна из участниц исследования Аманда Эдвардс, сообщает лондонская газета Daily Mail. "Акса" составила и специальный рейтинг квартир с наиболее высоким риском ограбления: 84, 34, 33, 88, 94, 62, 53, 55, 82 и 23. Их жильцам, по мнению страховой компании, следует повысить уровень защиты от воров. А проживающим в квартирах 33, 34, 68, 22, 55, 92, 96, 36, 69 и 83 необходимо, по мнению компании, проверить эффективность работы противопожарной системы. Специалисты "Акса" также вычислили квартирный номер, который обладает самой позитивной аурой. Это - 91. Проживающим в подобных квартирах людям часто везет, в том числе и в лотерее http://atompups.livejournal.com/38575.html |
|
|
Рената Великий магистр Группа: Администраторы Сообщений: 30442 
|
Добавлено: 31-01-2014 19:30 |
|
No Man's Sky генерирует планеты и звёзды не как точки с цифровыми характеристиками веса, излучения, плотности, а полностью. То есть вместе с ландшафтом. При этом ландшафт - не кубически-упрощённый, как в Minecraft, а гиперреалистичный. Джунгли, моря, подводная жизнь океанов - описывать это бесполезно, это надо видеть. Уделите пару минут, посмотрите на ролик. Если игра выйдет - это будет новый уровень бегства. Блуждать по этим мирам можно будет вечно. Кубический Minecraft - и тот уже необозрим физически для одного человека. А тут будут миллионы планет и размер вселенной будет ограничен лишь объемом твоего жесткого диска, на который будут выгружаться генерируемые пространства по мере твоего бесконечного путешествия. http://kvisaz.livejournal.com/588208.html |


|
| средневековые замки / разное / Оптические иллюзии, виртуальные миры и др. математика |